Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AQA 7356/2 Jun 2022 AS Exam Q. 10 : 8 marks in 9:00 min.
AQA 7357/1 Nov 2021 A2 Exam Q. 1 : 1 mark in 1:12 min.
AQA 7356/2 Nov 2020 AS Exam Q. 2 : 1 mark in 1:08 min.
AQA 7357/3 Jun 2019 A2 Exam Q. 4 : 3 marks in 3:36 min.
AQA 7356/1 Jun 2017 AS Sample Exam Q. 2 : 1 mark in 1:08 min.
Edexcel 8MA0/01 Jun 2023 AS Exam Q. 15 : 7 marks in 8:24 min.
Edexcel 8MA0/01 Jun 2023 AS Exam Q. 8 : 5 marks in 6:00 min.
Edexcel 9MA0/02 Jan 2023 A2 Mock Q. 1 : 5 marks in 6:00 min.
Edexcel 9MA0/01 Jun 2022 A2 Exam Q. 11 : 7 marks in 8:24 min.
Edexcel 9MA0/01 Jun 2022 A2 Exam Q. 5 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jun 2022 A2 Exam Q. 6 : 6 marks in 7:12 min.
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 7 : 9 marks in 10:48 min.
Edexcel 9MA0/01 Dec 2021 A2 Mock Q. 10 bc : 7 marks in 8:24 min.
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 3 : 5 marks in 6:00 min.
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 1 : 3 marks in 3:36 min.
Edexcel 9MA0/01 Oct 2020 A2 Exam Q. 7 : 5 marks in 6:00 min.
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 8 : 6 marks in 7:12 min.
Edexcel 8MA0/01 May 2018 AS Mock Q. 12 : 8 marks in 9:36 min.
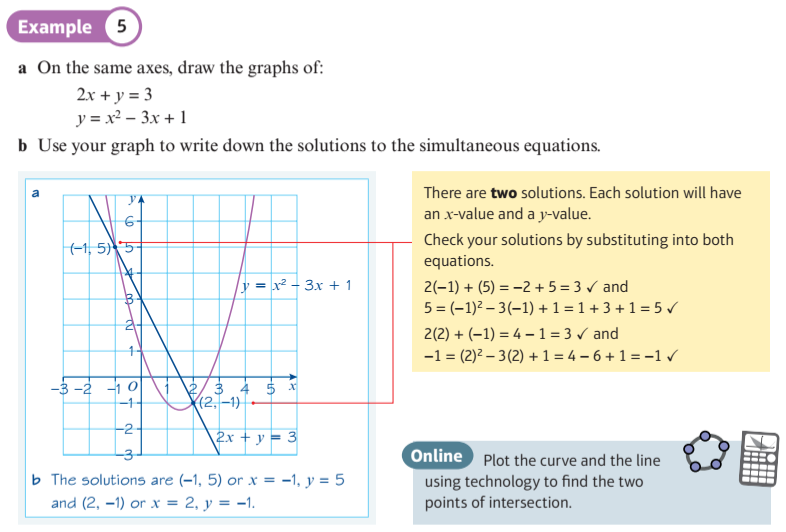
Check solutions to simultaneous equations
Find the point of intersection graphically
Plot the curve and the line to find the two points of intersection
Equations and inequalities: Page 44, Example 6
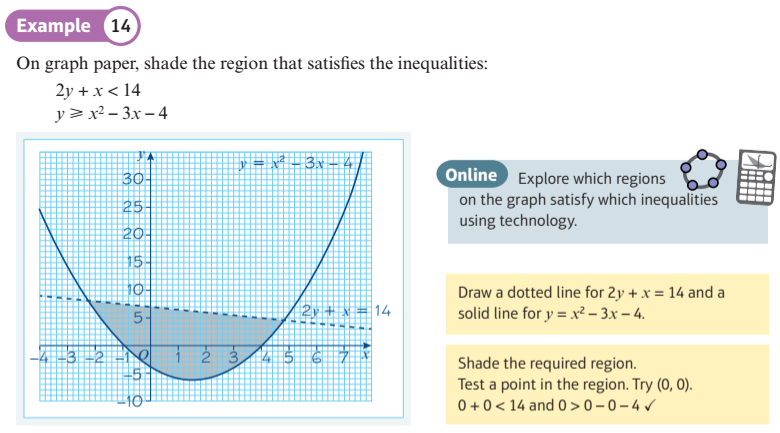
Explore which regions on the graph satisfy which inequalities
Solving Simultaneous Linear and Quadratic
Solution of simultaneous equations depends on whether or not their graphs intersect.
This display will help you understand how you can solve a Quadratic and Linear equation simultaneously.
You can find one or more common 'x's where the difference between the equations is zero, and then substitute these 'x's back into either equation to find the corresponding 'y's. The linear equation might be the simpler one to substitute your 'x' into, but it can be reassuring to check each 'x' and 'y' against both equations.
You can find one or more common 'x's where the difference between the equations is zero, and then substitute these 'x's back into either equation to find the corresponding 'y's. The linear equation might be the simpler one to substitute your 'x' into, but it can be reassuring to check each 'x' and 'y' against both equations.
Solving Two Simultaneous Quadratics
Solution of simultaneous equations depends on whether or not their graphs intersect.
This display will help you understand how you can solve two quadratic equations simultaneously;
one marked in blue and one marked in red.
You can find one or more common 'x's where the difference between the equations is zero, and then substitute these 'x's back into either equation to find the corresponding 'y's. It can be reassuring to check each 'x' and 'y' against both equations.
How many solutions can two simultaneous quadratics have; at least and at most?
You can find one or more common 'x's where the difference between the equations is zero, and then substitute these 'x's back into either equation to find the corresponding 'y's. It can be reassuring to check each 'x' and 'y' against both equations.
How many solutions can two simultaneous quadratics have; at least and at most?
Investigate Linear Inequalities
The inequality $ax + b > cx + d$ can be investigated in this display.
The line $y = ax + b$ is shown in blue and the line $y = cx + d$ is shown in red.
$ax + b > cx + d$ where the blue line lies above the red line.
The solution is shown on the number line at the bottom.
Note that the solution is itself an inequality, but in terms of just x.
Note also, that the intersection point is shown as an open circle on the number line, because it isn't itself included in the solution.
When the solution lies to the left of the intersection you should be able to see how the direction of an inequality reverses when multiplying or dividing both sides by a negative number.
The line $y = ax + b$ is shown in blue and the line $y = cx + d$ is shown in red.
$ax + b > cx + d$ where the blue line lies above the red line.
The solution is shown on the number line at the bottom.
Note that the solution is itself an inequality, but in terms of just x.
Note also, that the intersection point is shown as an open circle on the number line, because it isn't itself included in the solution.
When the solution lies to the left of the intersection you should be able to see how the direction of an inequality reverses when multiplying or dividing both sides by a negative number.
Investigate Quadratic Inequalities
The quadratic inequality $a{x^2} + bx + c < 0$ can be investigated in this display.
The curve $y = a{x^2} + bx + c < 0$ is plotted, and the inequality holds where this curve lies below the x-axis.
The solution is shown on the number line at the bottom.
Note that the solution is itself an inequality, but in terms of just x.
Note also, that intersection points are shown as open circles on the number line, because they aren't themselves included in the solution.
The curve $y = a{x^2} + bx + c < 0$ is plotted, and the inequality holds where this curve lies below the x-axis.
The solution is shown on the number line at the bottom.
Note that the solution is itself an inequality, but in terms of just x.
Note also, that intersection points are shown as open circles on the number line, because they aren't themselves included in the solution.
Investigate Quadratic/Linear Inequalities
The solutions to inequalities like $\color{green}{a{x^2} + bx + c \ge dx + e}$ can be illustrated graphically.
Both the curve $\color{blue}{y = a{x^2} + bx + c}$ and the line $\color{red}{y = dx + e}$ are plotted, and the inequality holds where the curve lies on or above the line.
The solution is shown on the number line at the bottom. Note that the solution is itself an inequality, but in terms of just x. Note also, that intersection points are shown as closed circles on the number line, because they are included in the solution.
Both the curve $\color{blue}{y = a{x^2} + bx + c}$ and the line $\color{red}{y = dx + e}$ are plotted, and the inequality holds where the curve lies on or above the line.
The solution is shown on the number line at the bottom. Note that the solution is itself an inequality, but in terms of just x. Note also, that intersection points are shown as closed circles on the number line, because they are included in the solution.