Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
Edexcel 8MA0/01 Apr 2023 AS Mock Q. 10 : 8 marks in 9:36 min.
Edexcel 8MA0/01 Apr 2023 AS Mock Q. 5 : 5 marks in 6:00 min.
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 14 : 8 marks in 9:36 min.
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 5 : 6 marks in 7:12 min.
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 4 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 12 : 9 marks in 10:48 min.
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 14 ab : 5 marks in 6:00 min.
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 2 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 6 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jun 2019 A2 Exam Q. 5 ab : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jun 2019 A2 Shadow Exam Q. 5 ab : 6 marks in 7:12 min.
Edexcel 8MA0/01 Jun 2019 AS Exam Q. 9 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 12 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 3 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Jun 2018 AS Exam Q. 6 : 7 marks in 8:24 min.
Edexcel 9MA0/02 Jun 2018 A2 Exam Q. 8 : 7 marks in 8:24 min.
Edexcel 8MA0/01 May 2018 AS Mock Q. 4 : 4 marks in 4:48 min.
Edexcel 9MA0/02 May 2018 A2 Mock Q. 5 : 5 marks in 6:00 min.
Edexcel 9MA0/01 May 2018 A2 Mock Q. 6 : 6 marks in 7:12 min.
Edexcel 8MA0/01 Jun 2017 AS Sample Exam Q. 10 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Jun 2017 AS Sample Exam Q. 4 b : 4 marks in 4:48 min.
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 11 : 9 marks in 10:48 min.
Check solutions of quadratic equations
Explore how the quadratic graph changes as the values of coefficients change
Explore how the value of the discriminant changes with the value of the constant
Explore the trajectory of the spear
Solving Quadratic Equations
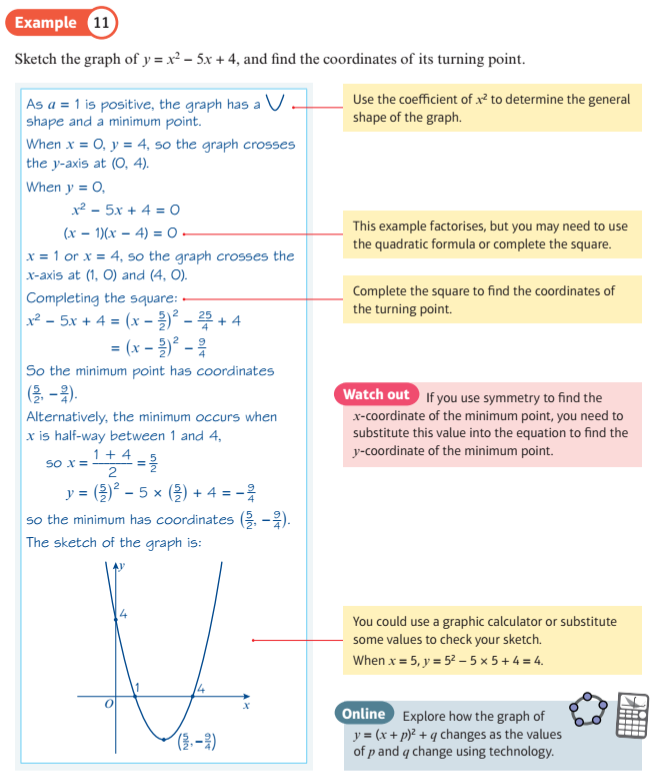
Equations like ${{x^2} - 8x + 15 = 0}$ can be solved by plotting ${y = {x^2} - 8x + 15}$ and seeing where the curve crosses the x-axis.
Solve each of the equations in the display below. You can use the green point to help you by dragging it to the x-axis (where y = 0).
Solve each of the equations in the display below. You can use the green point to help you by dragging it to the x-axis (where y = 0).
Matching Quadratic Factors
You can select ten green quadratic curves on this page.
Using the sliders to match the blue dashed curve to the green curve will reveal the equation in each case, but can you say what the equation is before making the match?
Looking at where the green curve crosses the x-axis should help you.
Using the sliders to match the blue dashed curve to the green curve will reveal the equation in each case, but can you say what the equation is before making the match?
Looking at where the green curve crosses the x-axis should help you.
Extension Quadratic Problem
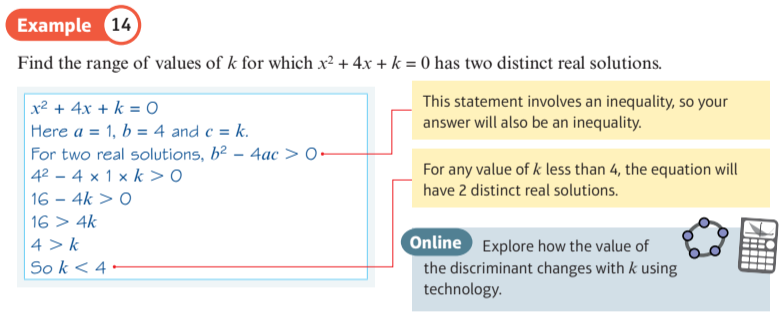
Find the set of values of $k$ for which $x$ is real, given that $y = {x^2} + kx + (2k - 3) = 0$
(a) For what values of k does the equation have:
(i) equal roots
(ii) roots of the same sign
(iii) roots of opposite sign?
(b) What is the significance of the common point on all the graphs?
(c) What is the greatest minimum value that the expression y can have, and for what value of k does this occur?
(d) Using your answers to (a) (i), can you find a curve which passes through the minimum point on each curve? (Hint: think about transformations of functions.)
(e) Now prove all your answers on paper.
(a) For what values of k does the equation have:
(i) equal roots
(ii) roots of the same sign
(iii) roots of opposite sign?
(b) What is the significance of the common point on all the graphs?
(c) What is the greatest minimum value that the expression y can have, and for what value of k does this occur?
(d) Using your answers to (a) (i), can you find a curve which passes through the minimum point on each curve? (Hint: think about transformations of functions.)
(e) Now prove all your answers on paper.