Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
Edexcel 9MA0/01 Jun 2023 A2 Exam Q. 5 : 6 marks in 7:12 min.
Edexcel 9MA0/02 Jan 2023 A2 Mock Q. 3 : 7 marks in 8:24 min.
Edexcel 9MA0/02 Jun 2022 A2 Exam Q. 5 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Dec 2021 A2 Mock Q. 3 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 11 a : 3 marks in 3:36 min.
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 1 : 5 marks in 6:00 min.
Edexcel 9MA0/01 Mar 2020 A2 Mock Q. 9 : 8 marks in 9:36 min.
Edexcel 9MA0/02 Jun 2019 A2 Exam Q. 2 : 4 marks in 4:48 min.
Edexcel 9MA0/02 Jun 2019 A2 Shadow Exam Q. 2 : 4 marks in 4:48 min.
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 1 : 5 marks in 6:00 min.
Edexcel 9MA0/01 May 2018 A2 Mock Q. 1 : 6 marks in 7:12 min.
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 14 ab : 4 marks in 4:48 min.
Under-estimation and over-estimation with the trapezium rule
Trapezium Rule Approximation for Difficult Integrals 1
The method of finding the area under a curve by splitting it up into strips is often referred to as a "Riemann
sum". The value of a definite integral can be estimated using various numerical
methods. This is particularly useful when the integral is difficult or
impossible to integrate. The method consists of dividing the area into strips.
The trapezium rule (or trapezoidal rule in the USA) is one such method. The
area of each strip is estimated by taking it to be approximately a
trapezium.
The trapezium method uses this formula:
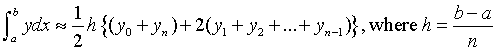
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
The trapezium method uses this formula:
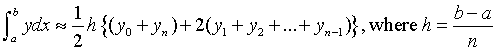
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
Trapezium Rule Approximation for Difficult Integrals 2
Functions such as $\color{blue}{y = {e^{ - {x^2}}}}$ and $\color{blue}{y = \sin \left( {x^2} \right)}$
cannot be integrated by basic methods.
However, their definite integrals can be estimated using numerical methods such as the trapezium rule (or trapezoidal rule in the USA) which is presented here.
The method consists of dividing the area into strips. The area of each strip is estimated by taking it to be approximately a trapezium.
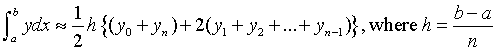
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
However, their definite integrals can be estimated using numerical methods such as the trapezium rule (or trapezoidal rule in the USA) which is presented here.
The method consists of dividing the area into strips. The area of each strip is estimated by taking it to be approximately a trapezium.
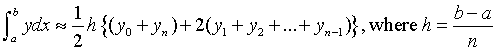
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.