Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
Edexcel 8MA0/01 Jun 2023 AS Exam Q. 3 : 4 marks in 4:48 min.
Edexcel 9MA0/01 Jun 2023 A2 Exam Q. 8 : 10 marks in 12:00 min.
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 2 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Jun 2022 AS Exam Q. 4 : 6 marks in 7:12 min.
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 6 a : 2 marks in 2:24 min.
Edexcel 9MA0/02 Nov 2021 A2 Exam Q. 6 : 5 marks in 6:00 min.
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 7 : 5 marks in 6:00 min.
Edexcel 8MA0/01 Oct 2020 AS Exam Q. 5 : 6 marks in 7:12 min.
Edexcel 9MA0/02 Mar 2020 A2 Mock Q. 3 : 9 marks in 10:48 min.
Edexcel 9MA0/02 Jun 2019 A2 Exam Q. 3 : 3 marks in 3:36 min.
Edexcel 9MA0/02 Jun 2019 A2 Shadow Exam Q. 3 : 3 marks in 3:36 min.
Edexcel 8MA0/01 Jun 2019 AS Exam Q. 6 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 2 : 5 marks in 6:00 min.
Edexcel 9MA0/01 Jun 2018 A2 Exam Q. 3 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Jun 2018 AS Exam Q. 7 : 6 marks in 7:12 min.
Edexcel 9MA0/02 May 2018 A2 Mock Q. 1 : 4 marks in 4:48 min.
Edexcel 8MA0/01 Jun 2017 AS Sample Exam Q. 8 : 5 marks in 6:00 min.
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 2 : 5 marks in 6:00 min.
Using trigonometrical functions
Using the radian mode for trigonometry
Evaluate inverse trigonometric functions in radians
Explore the Cosine Rule
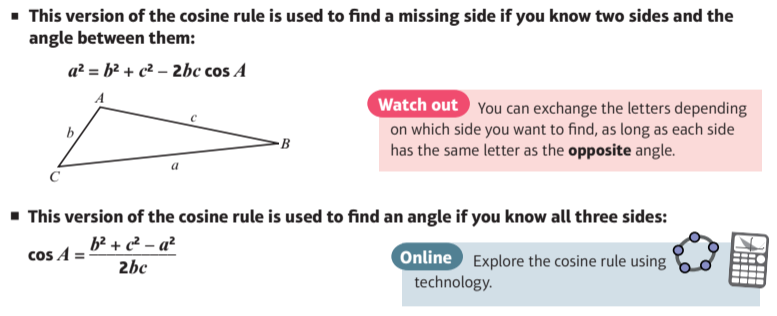
Explore the Sine Rule
Sin formula for the area of a triangle
Using Trig Rules: Page 188, Example 10
Explore the relationship between radians and arc lengths
Explore the relationship between radians and sector areas
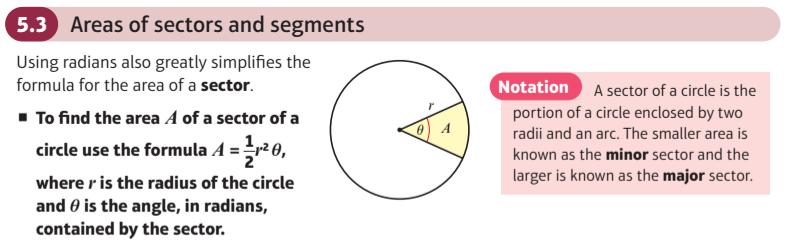
Explore the area of a segment
Explore transformations of sec, cosec and cot
Graphs of Reciprocal Trig: cosec, sec, cot
This display shows the graphs of the reciprocal trigonometric functions, cosec, sec and cot.
$\color{blue}{ cosec(a \, x) }$, $\color{blue}{ \sec(a \, x) }$ and $\color{blue}{ \cot(a \, x) }$ are plotted in blue for a coefficient $\color{blue}{ a }$ which you can change.
The reciprocal functions $\color{green}{ \sin(a \, x) }$, $\color{green}{ \cos(a \, x) }$ and $\color{green}{ \tan(a \, x) }$ are plotted in green alongside so you can see the reciprocal relationship.
You can also slide a red sample $\color{red}{ x }$ along the curves for a reading of corresponding values. Notice how the curves coincide at y = 1, because the reciprocal of 1 is 1.
$\color{blue}{ cosec(a \, x) }$, $\color{blue}{ \sec(a \, x) }$ and $\color{blue}{ \cot(a \, x) }$ are plotted in blue for a coefficient $\color{blue}{ a }$ which you can change.
The reciprocal functions $\color{green}{ \sin(a \, x) }$, $\color{green}{ \cos(a \, x) }$ and $\color{green}{ \tan(a \, x) }$ are plotted in green alongside so you can see the reciprocal relationship.
You can also slide a red sample $\color{red}{ x }$ along the curves for a reading of corresponding values. Notice how the curves coincide at y = 1, because the reciprocal of 1 is 1.
Introduction to Inverse Trigonometry
Suppose the value of sin(x), cos(x) or tan(x) is known.
Can we work backwards to find the value of x ?
This display shows that when we work backwards x can have many different values: an infinite number.
This display also shows that for sin(x) and cos(x) less than -1 or greater than +1, x has no possible values.
If sin(x) = t, x = arcsin(t).
If cos(x) = t, x = arccos(t).
If tan(x) = t, x = arccos(t).
In order that functions arcsin(t), arccos(t) and arctan(t) return a single 'principal' value, we have to restrict their ranges, by convention, as shown in a following display.
Finally, note that arcsin, arccos and arctan are commonly referred to as sin-1, cos-1 and tan-1, for instance on calculator keys. The '-1' indicates an inverse function, rather than a reciprocal index.
This display shows that when we work backwards x can have many different values: an infinite number.
This display also shows that for sin(x) and cos(x) less than -1 or greater than +1, x has no possible values.
If sin(x) = t, x = arcsin(t).
If cos(x) = t, x = arccos(t).
If tan(x) = t, x = arccos(t).
In order that functions arcsin(t), arccos(t) and arctan(t) return a single 'principal' value, we have to restrict their ranges, by convention, as shown in a following display.
Finally, note that arcsin, arccos and arctan are commonly referred to as sin-1, cos-1 and tan-1, for instance on calculator keys. The '-1' indicates an inverse function, rather than a reciprocal index.
Graphs of Inverse Trig: arcsin, arccos, arctan
This display allows you to investigate trigonometrical functions (in blue) and their inverses (in red).
Note that inverse trigonometrical functions, like all inverse functions, are reflections in the line 'y = x'.
Note also that because the trigonometrical functions are many-to-one, their inverses would be one-to-many, and therefore not true functions. In order to render the inverses as true functions, their ranges are restricted to a subset of "principal" values:
Note that inverse trigonometrical functions, like all inverse functions, are reflections in the line 'y = x'.
Note also that because the trigonometrical functions are many-to-one, their inverses would be one-to-many, and therefore not true functions. In order to render the inverses as true functions, their ranges are restricted to a subset of "principal" values:
| $ - {\pi \over 2} \le \arcsin (x) \le {\pi \over 2}$ | $0 \le \arccos (x) \le \pi$ | $ - {\pi \over 2} < \arctan (x) < {\pi \over 2}$ |
Investigate Inverses: arcsin(ax), arccos(ax), arctan(ax)
Use the display below to get familiar with the shapes of the graphs of the inverse functions $\color{red}{\arcsin (ax)}$, $\color{red}{\arccos (ax)}$ and $\color{red}{\arctan (ax)}$.
Note that these functions are also refered to as $\color{red}{\sin^{ - 1} (ax)}$, $\color{red}{\cos^{ - 1} (ax)}$ and $\color{red}{\tan^{ - 1} (ax)}$.
Inverse functions, are reflections in the line $\color{green}{y = x}$.
Is $\color{red}{\arcsin (ax)}$ always the inverse of $\color{blue}{\sin (ax)}$ ?
Note that these functions are also refered to as $\color{red}{\sin^{ - 1} (ax)}$, $\color{red}{\cos^{ - 1} (ax)}$ and $\color{red}{\tan^{ - 1} (ax)}$.
Inverse functions, are reflections in the line $\color{green}{y = x}$.
Is $\color{red}{\arcsin (ax)}$ always the inverse of $\color{blue}{\sin (ax)}$ ?
Sine/Cosine Graphs
This display allows you to view the shape and key features of Sine and Cosine curves.
You can drag a blue glider to read coordinates at a sample point.
This wave pattern occurs often in nature, including wind waves, sound waves, and light waves.
A cosine wave is said to be "sinusoidal", because $ \cos ( x ) = sin ( x + { \pi \over 2 } ) $, which is also a sine wave with a phase-shift of $ { \pi \over 2 } $ radians. Because of this "head start", it is often said that the cosine function leads the sine function or the sine lags the cosine.
The human ear can recognize single sine waves as sounding clear because sine waves are representations of a single frequency with no harmonics.
You can drag a blue glider to read coordinates at a sample point.
This wave pattern occurs often in nature, including wind waves, sound waves, and light waves.
A cosine wave is said to be "sinusoidal", because $ \cos ( x ) = sin ( x + { \pi \over 2 } ) $, which is also a sine wave with a phase-shift of $ { \pi \over 2 } $ radians. Because of this "head start", it is often said that the cosine function leads the sine function or the sine lags the cosine.
The human ear can recognize single sine waves as sounding clear because sine waves are representations of a single frequency with no harmonics.