Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
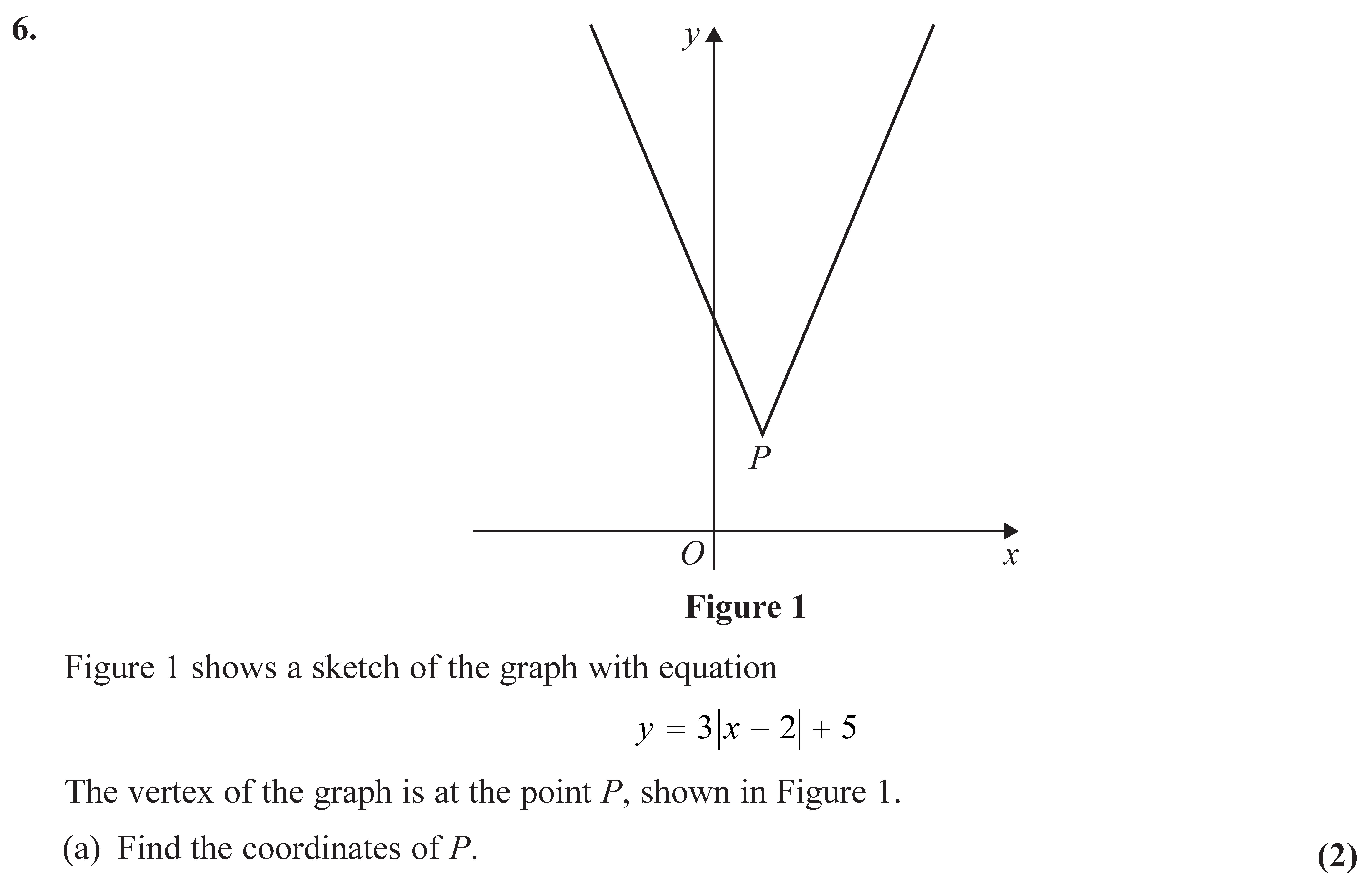
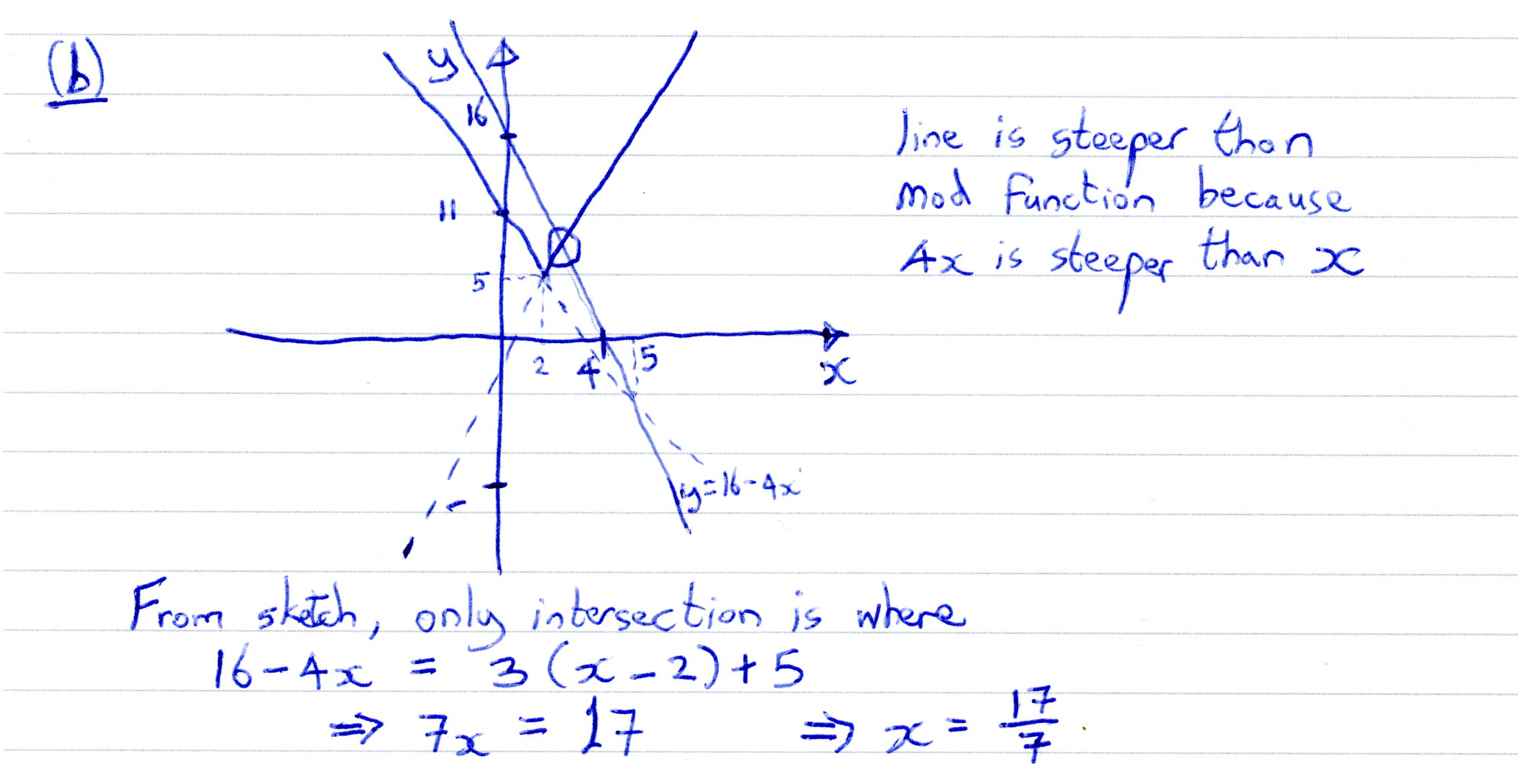
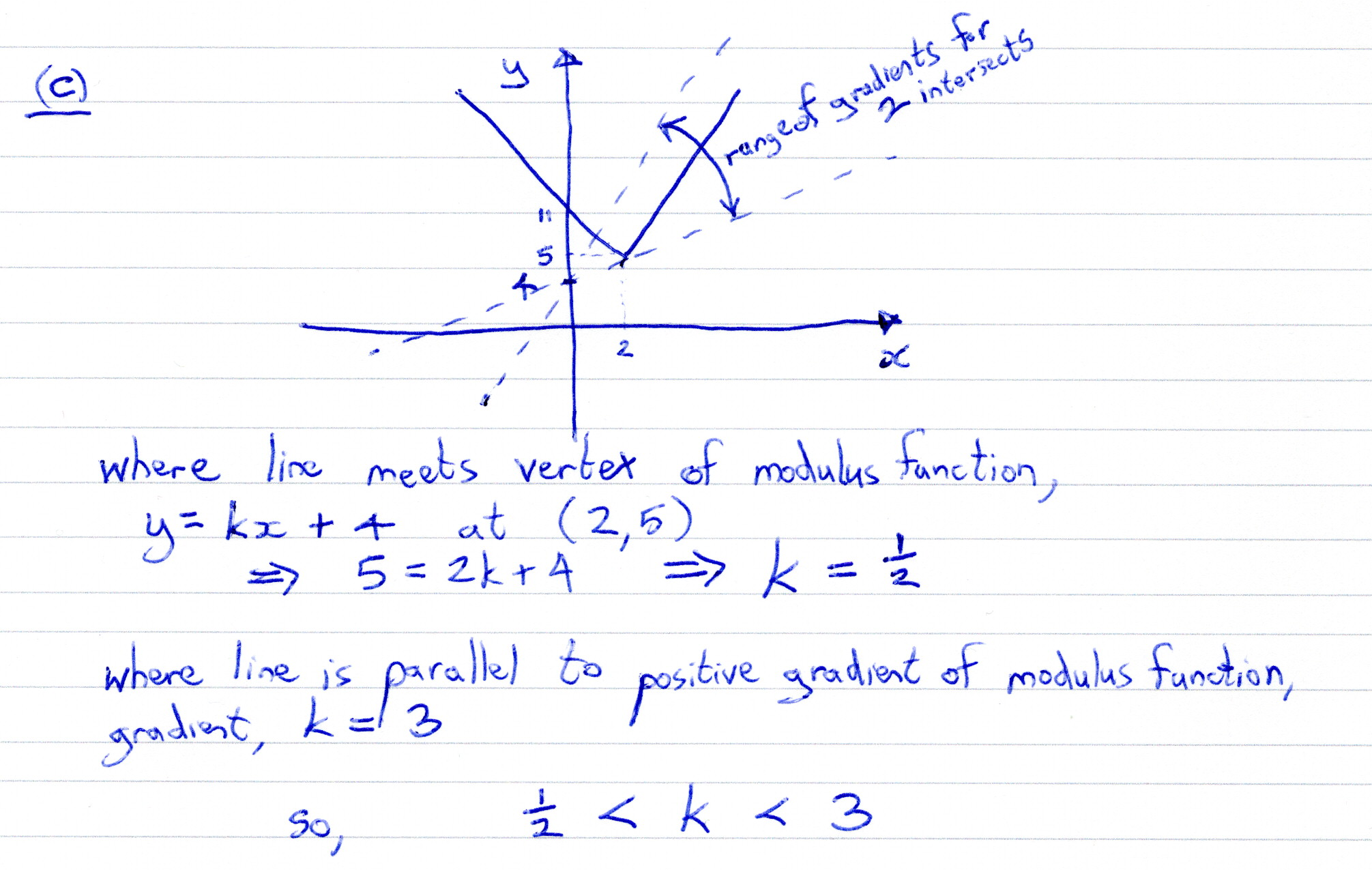
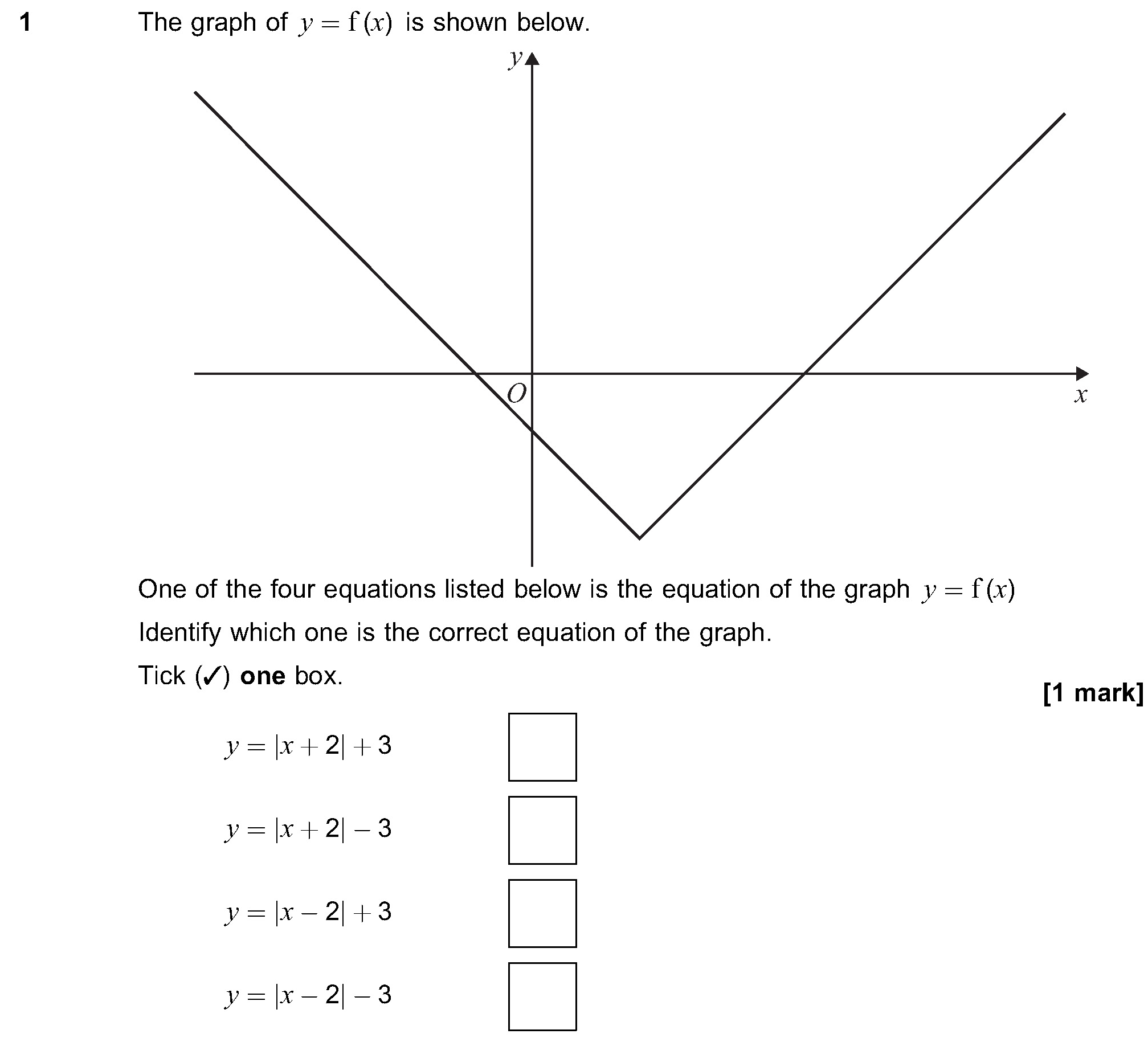
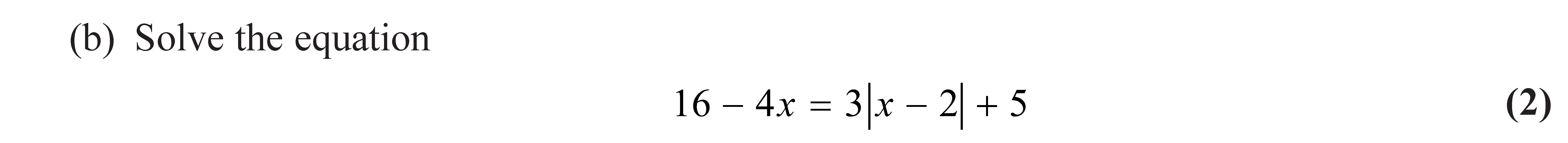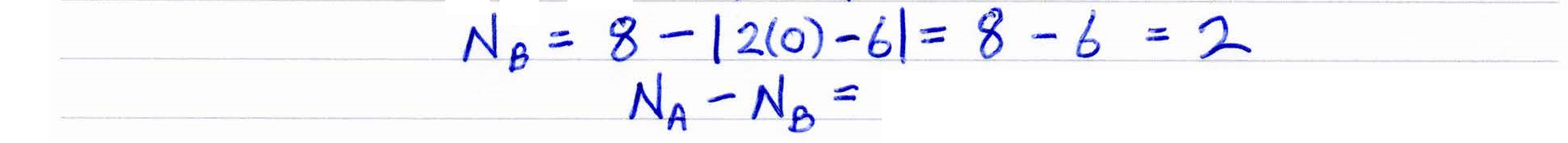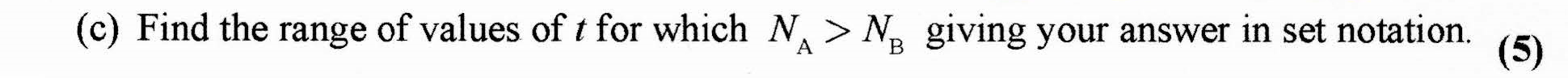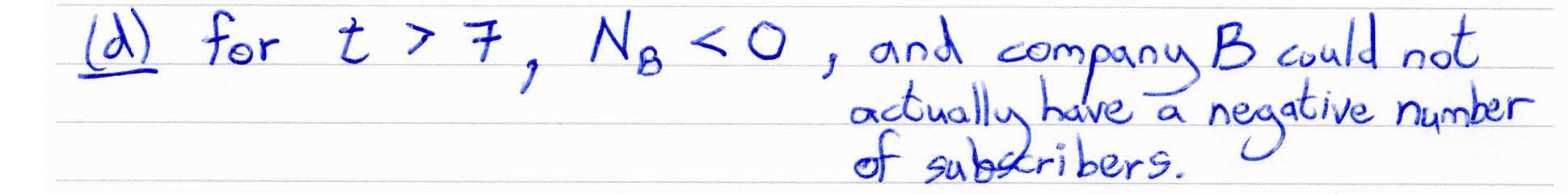OCR (A) H240/01 Jun 2024 A2 Exam Q. 8 : 7 marks in 8:24 min.
OCR (A) H240/03 Jun 2022 A2 Exam Q. 1 : 3 marks in 3:36 min.
OCR (A) H240/03 Nov 2021 A2 Exam Q. 4 : 5 marks in 6:00 min.
OCR (A) H240/01 Nov 2020 A2 Exam Q. 9 : 9 marks in 10:48 min.
OCR (A) H240/03 Jun 2019 A2 Exam Q. 3 a : 4 marks in 4:48 min.
OCR (A) H240/03 Jun 2018 A2 Exam Q. 2 : 3 marks in 3:36 min.
OCR (A) H240/03 Jun 2017 A2 Sample Exam Q. 1 : 7 marks in 8:24 min.
Edexcel 9MA0/01 Jun 2024 A2 Exam Q. 6 : 6 marks in 7:12 min.
Edexcel 9MA0/01 Jan 2024 A2 Mock Q. 10 : 9 marks in 10:48 min.
Edexcel 9MA0/02 Jun 2023 A2 Exam Q. 12 : 10 marks in 12:00 min.
Edexcel 9MA0/02 Jun 2022 A2 Exam Q. 1 : 4 marks in 4:48 min.
Edexcel 9MA0/01 Dec 2021 A2 Mock Q. 10 a : 2 marks in 2:24 min.
Edexcel 9MA0/02 Nov 2021 A2 Exam Q. 11 : 10 marks in 12:00 min.
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 11 : 7 marks in 8:24 min.
Edexcel 9MA0/01 Mar 2020 A2 Mock Q. 10 : 8 marks in 9:36 min.
Edexcel 9MA0/02 Jan 2019 A2 Mock Q. 5 : 5 marks in 6:00 min.
Edexcel 9MA0/02 Jun 2018 A2 Exam Q. 3 b : 3 marks in 3:36 min.
Edexcel 9MA0/02 May 2018 A2 Mock Q. 4 : 6 marks in 7:12 min.
Edexcel 9MA0/02 May 2017 A2 Sample Exam Q. 11 : 6 marks in 7:12 min.
AQA 7357/3 Jun 2023 A2 Exam Q. 1 : 1 mark in 1:12 min.
AQA 7357/2 Nov 2021 A2 Exam Q. 4 : 6 marks in 7:12 min.
AQA 7357/1 Nov 2020 A2 Exam Q. 4 : 5 marks in 6:00 min.
AQA 7357/2 Jun 2019 A2 Exam Q. 1 : 1 mark in 1:12 min.
AQA 7357/3 Jun 2018 A2 Exam Q. 4 : 3 marks in 3:36 min.
Using modulus functions
The modulus function
Intersections of straight lines and modulus graphs
Explore modulus transformations
Explore the solution to an inequality of a modulus function.
Investigate Modulus Inequalities 1
The modulus inequality $ { a \, { x ^ 2 } + b \, x + c > \left| \, d \, x + e \, \right| } $ can be investigated in this display.
$\color{blue}{ f(x) = a \, { x ^ 2 } + b \, x + c }$ is shown in blue and $\color{red}{g(x) = \left| \, d \, x + e \, \right| }$ is shown in red.
The solution is values of $x$ for which $\color{blue}{f(x)}$ lies above $\color{red}{g(x)}$.
$\color{blue}{ f(x) = a \, { x ^ 2 } + b \, x + c }$ is shown in blue and $\color{red}{g(x) = \left| \, d \, x + e \, \right| }$ is shown in red.
The solution is values of $x$ for which $\color{blue}{f(x)}$ lies above $\color{red}{g(x)}$.
Investigate Modulus Inequalities 2
The solutions to quadratic modulus inequalities like $\color{green}{\left| \, a \, {x^2} + b \, x + c \, \right| > d \, x + e}$ can be illustrated graphically.
Both the curve $\color{blue}{y = \left| \, a \, {x^2} + b \, x + c \, \right|}$ and the line $\color{red}{y = d \, x + e}$ are plotted, and the inequality holds where the modulus of the curve lies above the line.
The solution is shown on the number line at the bottom. Note that the solution is itself an inequality, but in terms of just x. Note also, that intersection points are shown as open circles on the number line, because they are not included in the solution.
Both the curve $\color{blue}{y = \left| \, a \, {x^2} + b \, x + c \, \right|}$ and the line $\color{red}{y = d \, x + e}$ are plotted, and the inequality holds where the modulus of the curve lies above the line.
The solution is shown on the number line at the bottom. Note that the solution is itself an inequality, but in terms of just x. Note also, that intersection points are shown as open circles on the number line, because they are not included in the solution.