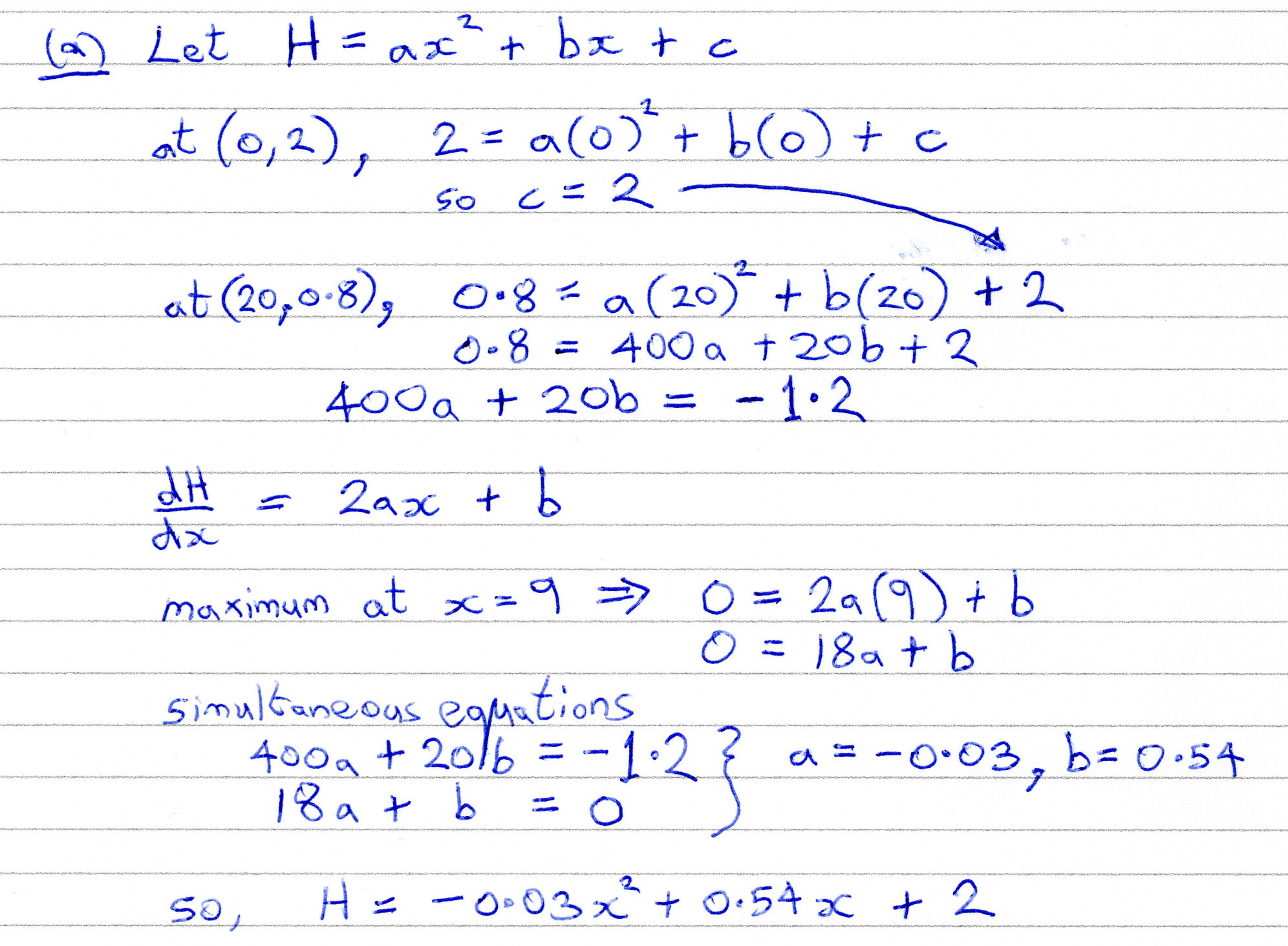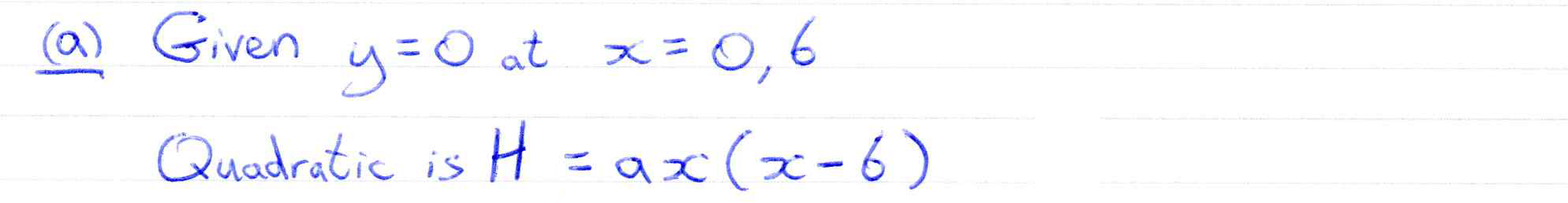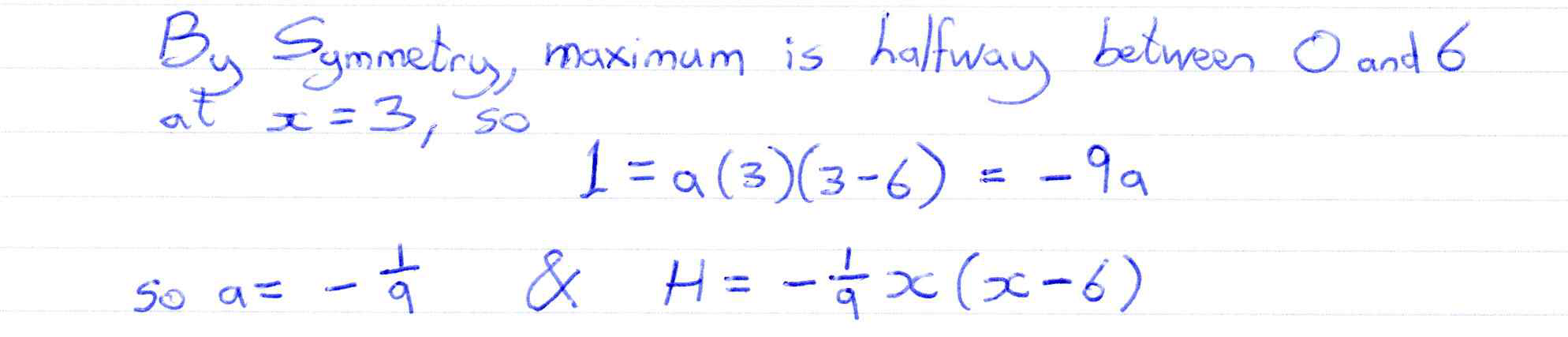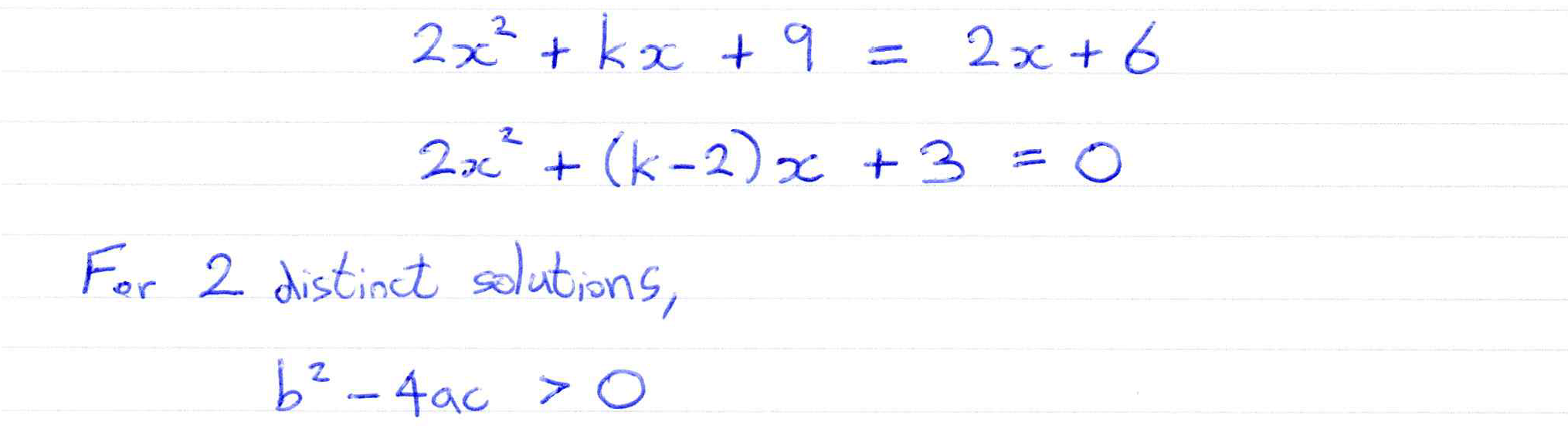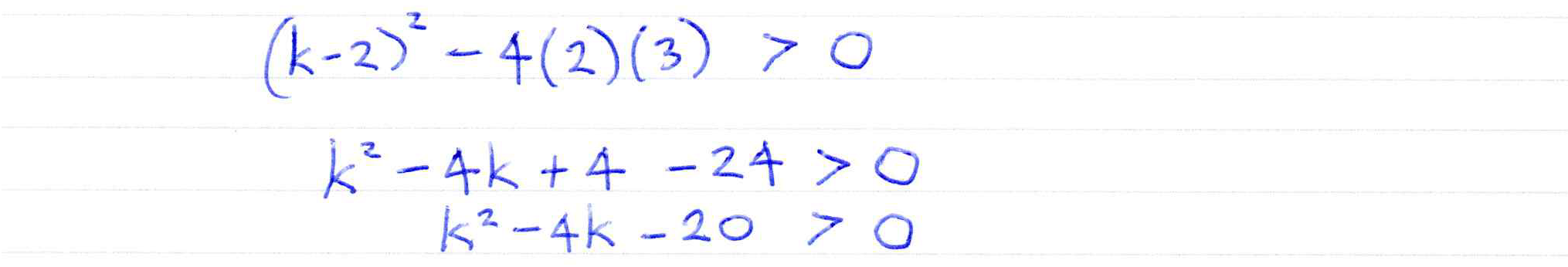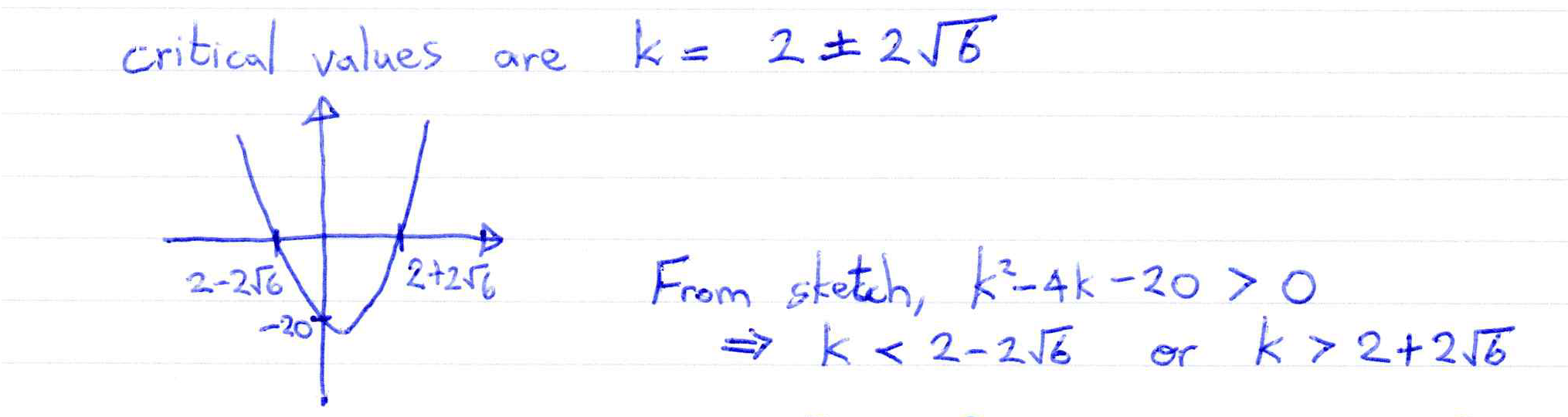Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads

- Theory Theory Revision
- OCR (A) Qs OCR (A) Qs
- Edexcel Qs Edexcel Qs
- AQA Qs AQA Qs
- OCR MEI Qs OCR MEI Qs
- fx-991EX Use of fx-991EX
- GeoGebra GeoGebra
- JsxGraph JsxGraph
-
Jun 24 AS
P2 Q 3 Jun 24 AS
Jun 24 AS
P2 Q 3
-
Jun 23 AS
P2 Q 1 Jun 23 AS
Jun 23 AS
P2 Q 1
-
Jun 23 A2
P2 Q 1 Jun 23 A2
Jun 23 A2
P2 Q 1
-
Jun 23 AS
P1 Q 6 a Jun 23 AS
Jun 23 AS
P1 Q 6 a
-
Jun 22 AS
P2 Q 2 Jun 22 AS
Jun 22 AS
P2 Q 2
-
Nov 21 A2
P1 Q 1 Nov 21 A2
Nov 21 A2
P1 Q 1
-
Jun 19 AS
P1 Q 2 Jun 19 AS
Jun 19 AS
P1 Q 2
-
Jun 18 A2
P2 Q 1 Jun 18 A2
Jun 18 A2
P2 Q 1
-
Jun 18 AS
P1 Q 2 Jun 18 AS
Jun 18 AS
P1 Q 2
-
Jun 18 A2
P1 Q 3 Jun 18 A2
Jun 18 A2
P1 Q 3
-
Jun 18 AS
P2 Q 4 Jun 18 AS
Jun 18 AS
P2 Q 4
-
Jun 17 A2
P2 Q 3 Jun 17 A2
Jun 17 A2
P2 Q 3
-
Jun 17 AS
P1 Q 7 Jun 17 AS
Jun 17 AS
P1 Q 7
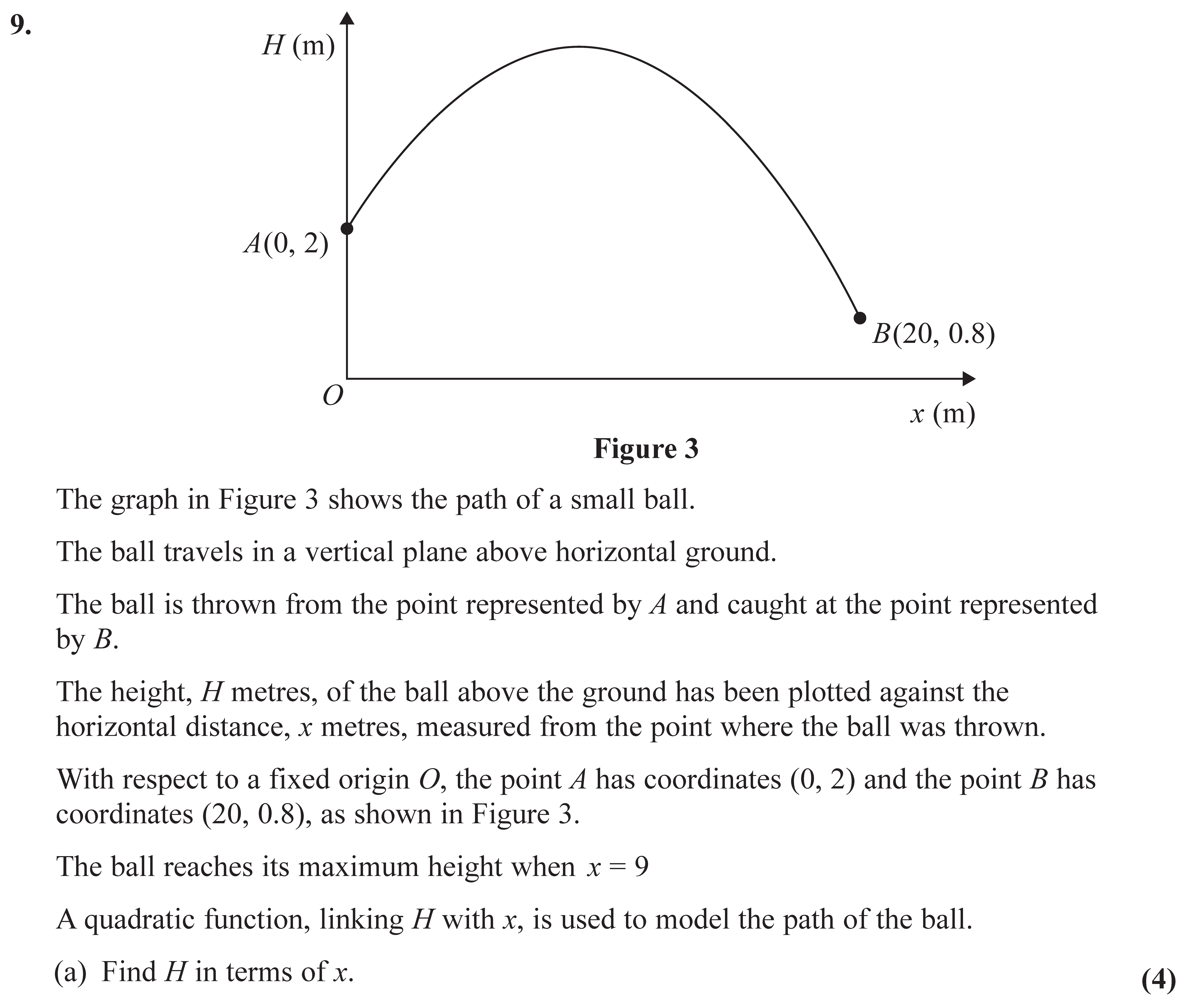
OCR (A) H230/02 Jun 2024 AS Exam Q. 3
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/02 Jun 2023 AS Exam Q. 1
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Jun 2023 A2 Exam Q. 1
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/01 Jun 2023 AS Exam Q. 6 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/02 Jun 2022 AS Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/01 Nov 2021 A2 Exam Q. 1
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/01 Jun 2019 AS Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Jun 2018 A2 Exam Q. 1
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/01 Jun 2018 AS Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/01 Jun 2018 A2 Exam Q. 3
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/02 Jun 2018 AS Exam Q. 4
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Jun 2017 A2 Sample Exam Q. 3
 9 marks in 10:48 min.
9 marks in 10:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/01 Jun 2017 AS Sample Exam Q. 7
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 25 A2
P2 Q 1 Jun 25 A2
Jun 25 A2
P2 Q 1
-
Jun 25 AS
Q 7 Jun 25 AS
Jun 25 AS
Q 7
-
Jun 25 AS
Q 9 Jun 25 AS
Jun 25 AS
Q 9
-
Dec 24 AS
Q 1 Dec 24 AS
Dec 24 AS
Q 1
-
Dec 24 AS
Q 5 Dec 24 AS
Dec 24 AS
Q 5
-
Jun 24 A2
P2 Q 9 Jun 24 A2
Jun 24 A2
P2 Q 9
-
Jan 24 A2
P2 Q 10 Jan 24 A2
Jan 24 A2
P2 Q 10
-
Apr 23 AS
Q 10 Apr 23 AS
Apr 23 AS
Q 10
-
Apr 23 AS
Q 5 Apr 23 AS
Apr 23 AS
Q 5
-
Jun 22 AS
Q 14 Jun 22 AS
Jun 22 AS
Q 14
-
Jun 22 AS
Q 5 Jun 22 AS
Jun 22 AS
Q 5
-
Dec 21 A2
P2 Q 4 Dec 21 A2
Dec 21 A2
P2 Q 4
-
Nov 21 A2
P1 Q 12 Nov 21 A2
Nov 21 A2
P1 Q 12
-
Nov 21 AS
Q 14 ab Nov 21 AS
Nov 21 AS
Q 14 ab
-
Nov 21 A2
P1 Q 2 Nov 21 A2
Nov 21 A2
P1 Q 2
-
Nov 21 AS
Q 6 Nov 21 AS
Nov 21 AS
Q 6
-
Jun 19 A2
P1 Q 5 ab Jun 19 A2
Jun 19 A2
P1 Q 5 ab
-
Jun 19 A2
P1 Q 5 ab Jun 19 A2
Jun 19 A2
P1 Q 5 ab
-
Jun 19 AS
Q 9 Jun 19 AS
Jun 19 AS
Q 9
-
Jan 19 A2
P1 Q 12 Jan 19 A2
Jan 19 A2
P1 Q 12
-
Jan 19 A2
P1 Q 3 Jan 19 A2
Jan 19 A2
P1 Q 3
-
Jun 18 AS
Q 6 Jun 18 AS
Jun 18 AS
Q 6
-
Jun 18 A2
P2 Q 8 Jun 18 A2
Jun 18 A2
P2 Q 8
-
May 18 AS
Q 4 May 18 AS
May 18 AS
Q 4
-
May 18 A2
P2 Q 5 May 18 A2
May 18 A2
P2 Q 5
-
May 18 A2
P1 Q 6 May 18 A2
May 18 A2
P1 Q 6
-
Jun 17 AS
Q 10 Jun 17 AS
Jun 17 AS
Q 10
-
Jun 17 AS
Q 4 b Jun 17 AS
Jun 17 AS
Q 4 b
-
May 17 A2
P1 Q 11 May 17 A2
May 17 A2
P1 Q 11
Edexcel 9MA0/02 Jun 2025 A2 Exam Q. 1
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (1)
Request * Pop-Up Working * (1)
Edexcel 8MA0/01 Jun 2025 AS Exam Q. 7
 10 marks in 12:00 min.
10 marks in 12:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2025 AS Exam Q. 9
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Dec 2024 AS Mock Q. 1
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Dec 2024 AS Mock Q. 5
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2024 A2 Exam Q. 9
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2024 A2 Mock Q. 10
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Apr 2023 AS Mock Q. 10
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Apr 2023 AS Mock Q. 5
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 14
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2022 AS Mock Q. 5
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 4
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 12
 9 marks in 10:48 min.
9 marks in 10:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 14 ab
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Nov 2021 AS Exam Q. 6
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Exam Q. 5 ab
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Shadow Exam Q. 5 ab
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2019 AS Exam Q. 9
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 12
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 3
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2018 AS Exam Q. 6
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2018 A2 Exam Q. 8
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 May 2018 AS Mock Q. 4
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 May 2018 A2 Mock Q. 5
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 May 2018 A2 Mock Q. 6
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2017 AS Sample Exam Q. 10
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 8MA0/01 Jun 2017 AS Sample Exam Q. 4 b
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 11
 9 marks in 10:48 min.
9 marks in 10:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 24 A2
P3 Q 2 Jun 24 A2
Jun 24 A2
P3 Q 2
-
Jun 23 A2
P2 Q 1 Jun 23 A2
Jun 23 A2
P2 Q 1
-
Jun 22 AS
P2 Q 4 Jun 22 AS
Jun 22 AS
P2 Q 4
-
Nov 21 A2
P2 Q 1 Nov 21 A2
Nov 21 A2
P2 Q 1
-
Nov 20 AS
P2 Q 11 Nov 20 AS
Nov 20 AS
P2 Q 11
-
Jun 18 A2
P2 Q 4 Jun 18 A2
Jun 18 A2
P2 Q 4
-
Jun 18 AS
P2 Q 7 Jun 18 AS
Jun 18 AS
P2 Q 7
-
Jun 17 AS
P2 Q 4 Jun 17 AS
Jun 17 AS
P2 Q 4
-
Jun 17 AS
P2 Q 5 Jun 17 AS
Jun 17 AS
P2 Q 5
-
Jun 17 A2
P2 Q 6 Jun 17 A2
Jun 17 A2
P2 Q 6
-
Jun 17 A2
P1 Q 7 Jun 17 A2
Jun 17 A2
P1 Q 7
AQA 7357/3 Jun 2024 A2 Exam Q. 2
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/2 Jun 2023 A2 Exam Q. 1
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2022 AS Exam Q. 4
 4 marks in 4:30 min.
4 marks in 4:30 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/2 Nov 2021 A2 Exam Q. 1
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Nov 2020 AS Exam Q. 11
 11 marks in 12:22 min.
11 marks in 12:22 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/2 Jun 2018 A2 Exam Q. 4
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2018 AS Exam Q. 7
 6 marks in 6:45 min.
6 marks in 6:45 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2017 AS Sample Exam Q. 4
 3 marks in 3:22 min.
3 marks in 3:22 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2017 AS Sample Exam Q. 5
 4 marks in 4:30 min.
4 marks in 4:30 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/2 Jun 2017 A2 Sample Exam Q. 6
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2017 A2 Sample Exam Q. 7
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 24 AS
P2 Q 2 Jun 24 AS
Jun 24 AS
P2 Q 2
-
Jun 24 AS
P2 Q 8 Jun 24 AS
Jun 24 AS
P2 Q 8
-
Jun 23 AS
P2 Q 15 Jun 23 AS
Jun 23 AS
P2 Q 15
-
Jun 23 AS
P2 Q 2 Jun 23 AS
Jun 23 AS
P2 Q 2
-
Jun 22 AS
P2 Q 2 Jun 22 AS
Jun 22 AS
P2 Q 2
-
Jun 22 AS
P1 Q 3 Jun 22 AS
Jun 22 AS
P1 Q 3
-
Nov 21 A2
P3 Q 1 Nov 21 A2
Nov 21 A2
P3 Q 1
-
Jun 19 AS
P1 Q 1 Jun 19 AS
Jun 19 AS
P1 Q 1
-
Jun 18 AS
P2 Q 5 Jun 18 AS
Jun 18 AS
P2 Q 5
-
Jun 18 A2
P3 Q 7 Jun 18 A2
Jun 18 A2
P3 Q 7
-
Jun 17 AS
P1 Q 11 Jun 17 AS
Jun 17 AS
P1 Q 11
-
Jun 17 A2
P1 Q 13 Jun 17 A2
Jun 17 A2
P1 Q 13
-
Jun 17 AS
P1 Q 4 Jun 17 AS
Jun 17 AS
P1 Q 4
OCR MEI H630/02 Jun 2024 AS Exam Q. 2
 3 marks in 3:52 min.
3 marks in 3:52 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/02 Jun 2024 AS Exam Q. 8
 4 marks in 5:09 min.
4 marks in 5:09 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/02 Jun 2023 AS Exam Q. 15
 7 marks in 8:60 min.
7 marks in 8:60 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/02 Jun 2023 AS Exam Q. 2
 3 marks in 3:51 min.
3 marks in 3:51 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/02 Jun 2022 AS Exam Q. 2
 4 marks in 5:09 min.
4 marks in 5:09 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/01 Jun 2022 AS Exam Q. 3
 3 marks in 3:52 min.
3 marks in 3:52 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/03 Nov 2021 A2 Exam Q. 1
 5 marks in 8:00 min.
5 marks in 8:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/01 Jun 2019 AS Exam Q. 1
 3 marks in 3:52 min.
3 marks in 3:52 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/02 Jun 2018 AS Exam Q. 5
 3 marks in 3:52 min.
3 marks in 3:52 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/03 Jun 2018 A2 Exam Q. 7
 8 marks in 12:48 min.
8 marks in 12:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/01 Jun 2017 AS Sample Exam Q. 11
 6 marks in 7:43 min.
6 marks in 7:43 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Jun 2017 A2 Exam Q. 13
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H630/01 Jun 2017 AS Sample Exam Q. 4
 3 marks in 3:51 min.
3 marks in 3:51 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
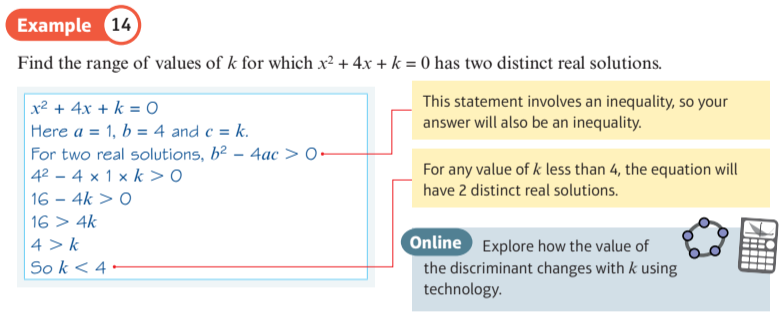
Check solutions of quadratic equations

Explore how the quadratic graph changes as the values of coefficients change
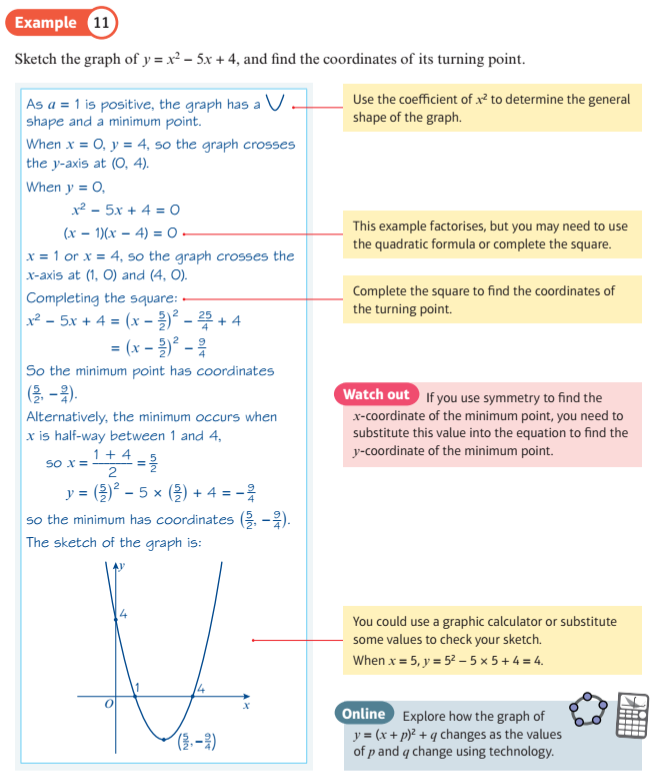
Explore how the value of the discriminant changes with the value of the constant
Explore the trajectory of the spear

- Solving Quadratics (AS) Solving Quadratics (AS)
- Matching Factors (AS) Matching Factors (AS)
- Extension Problem (Ext) Extension Problem (Ext)
Solving Quadratic Equations
Equations like ${{x^2} - 8x + 15 = 0}$ can be solved by plotting ${y = {x^2} - 8x + 15}$ and seeing where the curve crosses the x-axis.
Solve each of the equations in the display below. You can use the green point to help you by dragging it to the x-axis (where y = 0).
Solve each of the equations in the display below. You can use the green point to help you by dragging it to the x-axis (where y = 0).
Matching Quadratic Factors
You can select ten green quadratic curves on this page.
Using the sliders to match the blue dashed curve to the green curve will reveal the equation in each case, but can you say what the equation is before making the match?
Looking at where the green curve crosses the x-axis should help you.
Using the sliders to match the blue dashed curve to the green curve will reveal the equation in each case, but can you say what the equation is before making the match?
Looking at where the green curve crosses the x-axis should help you.
Extension Quadratic Problem
Find the set of values of $k$ for which $x$ is real, given that $y = {x^2} + kx + (2k - 3) = 0$
(a) For what values of k does the equation have:
(i) equal roots
(ii) roots of the same sign
(iii) roots of opposite sign?
(b) What is the significance of the common point on all the graphs?
(c) What is the greatest minimum value that the expression y can have, and for what value of k does this occur?
(d) Using your answers to (a) (i), can you find a curve which passes through the minimum point on each curve? (Hint: think about transformations of functions.)
(e) Now prove all your answers on paper.
(a) For what values of k does the equation have:
(i) equal roots
(ii) roots of the same sign
(iii) roots of opposite sign?
(b) What is the significance of the common point on all the graphs?
(c) What is the greatest minimum value that the expression y can have, and for what value of k does this occur?
(d) Using your answers to (a) (i), can you find a curve which passes through the minimum point on each curve? (Hint: think about transformations of functions.)
(e) Now prove all your answers on paper.