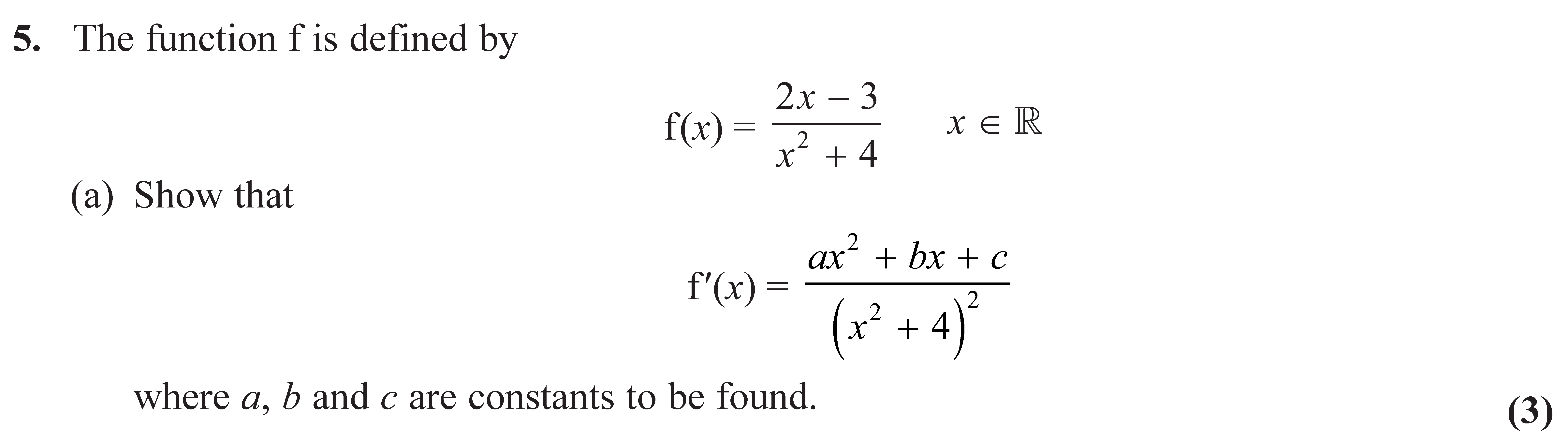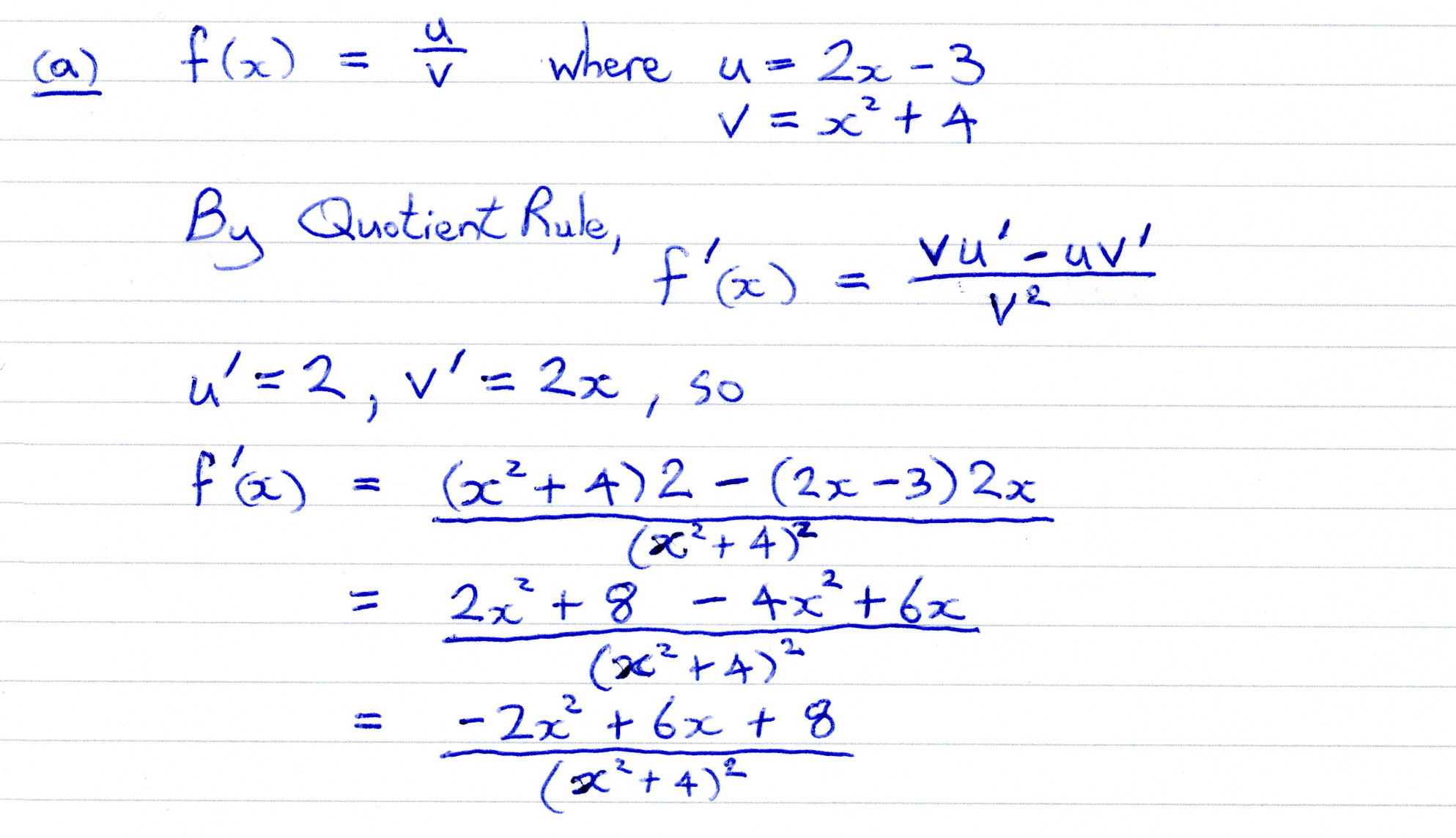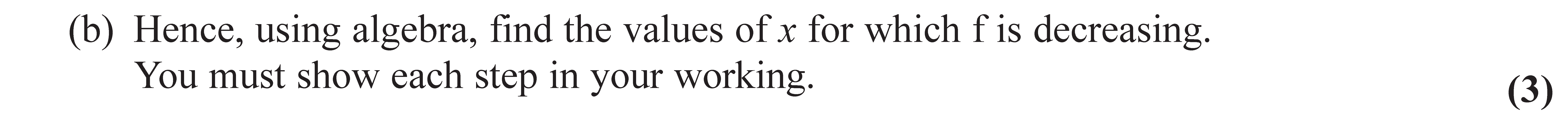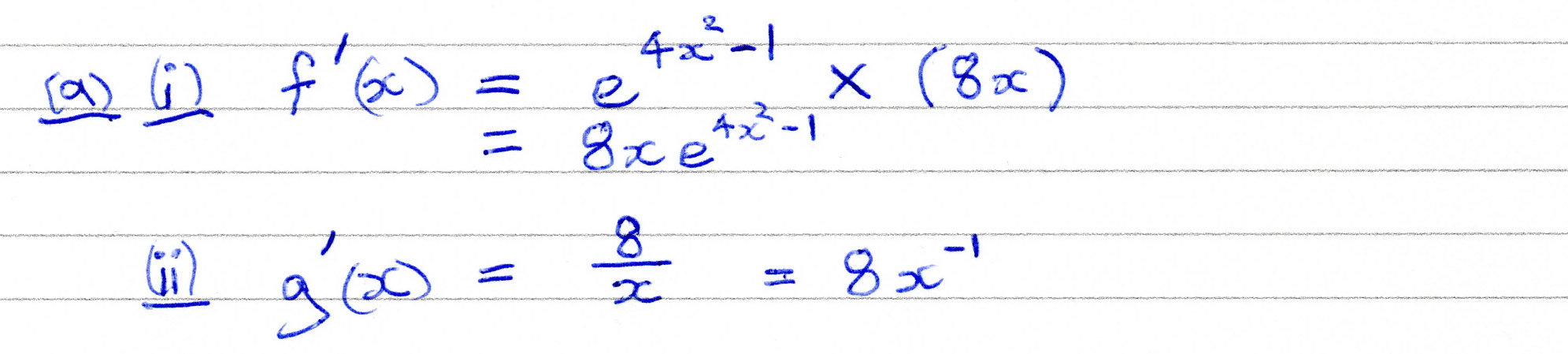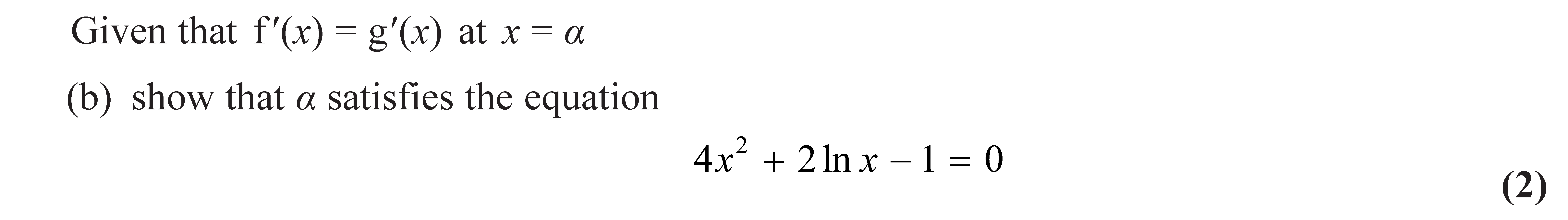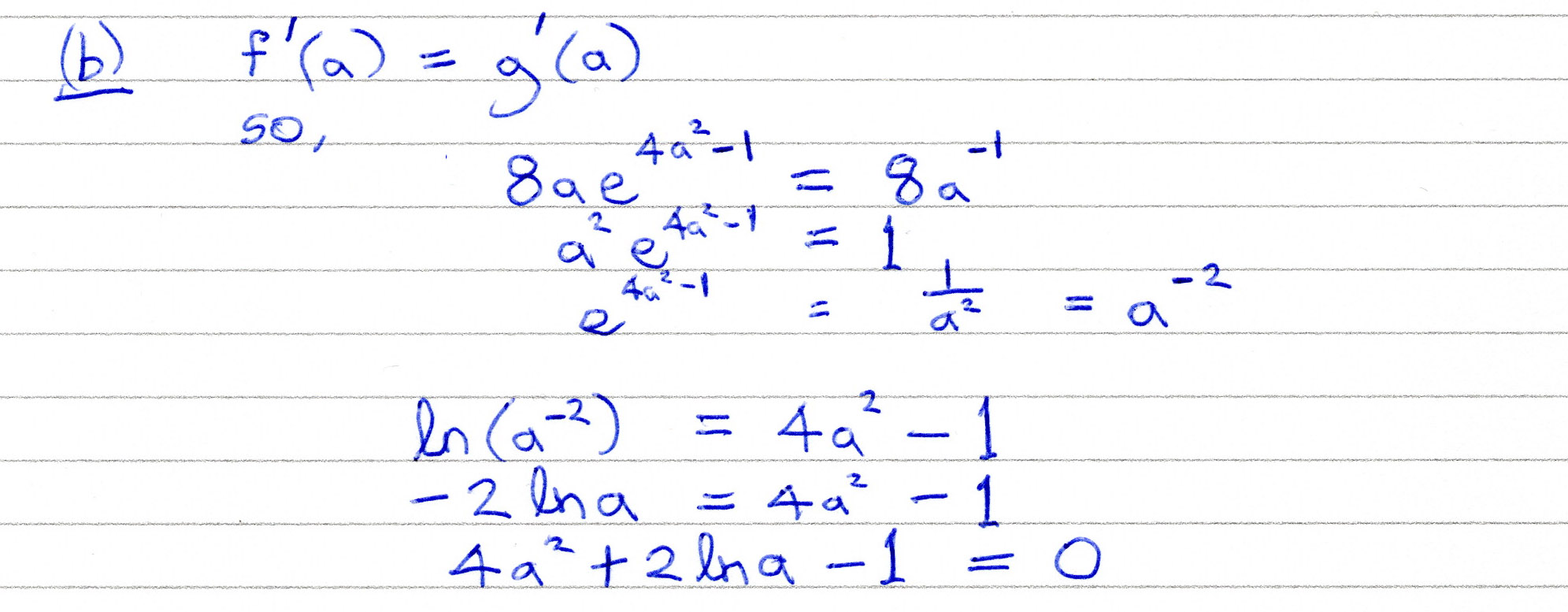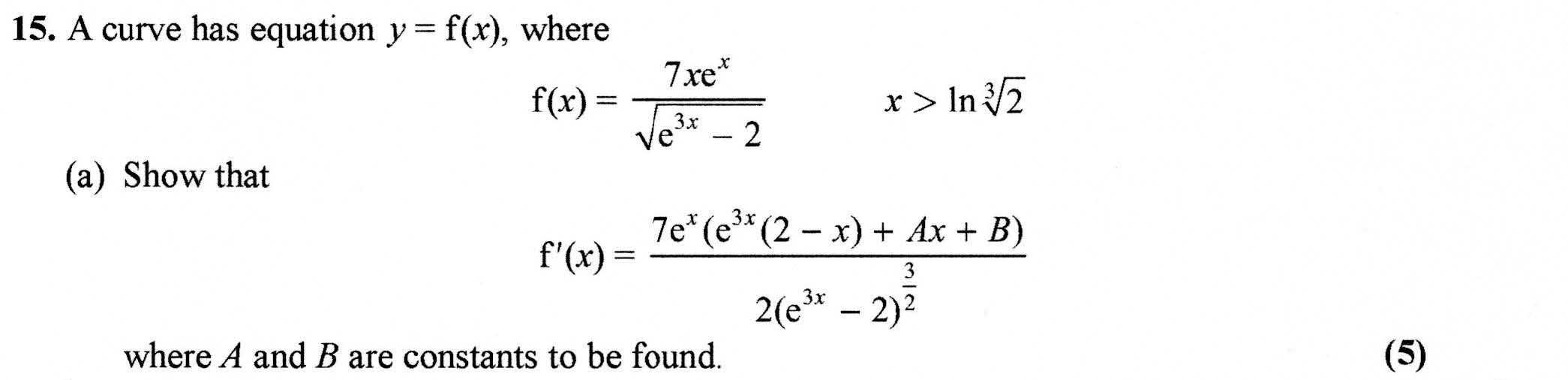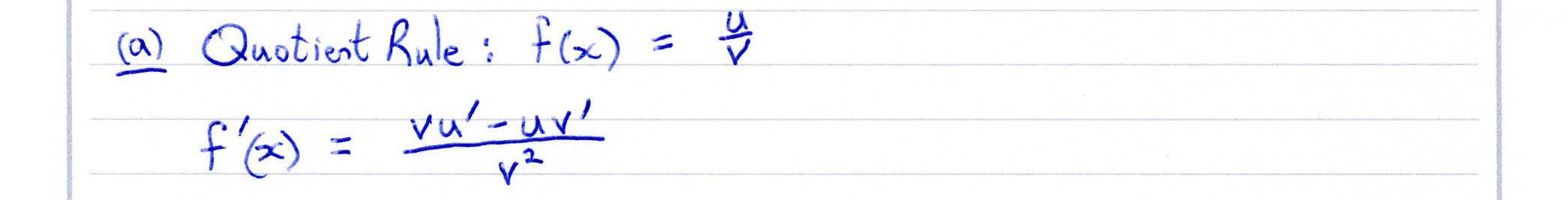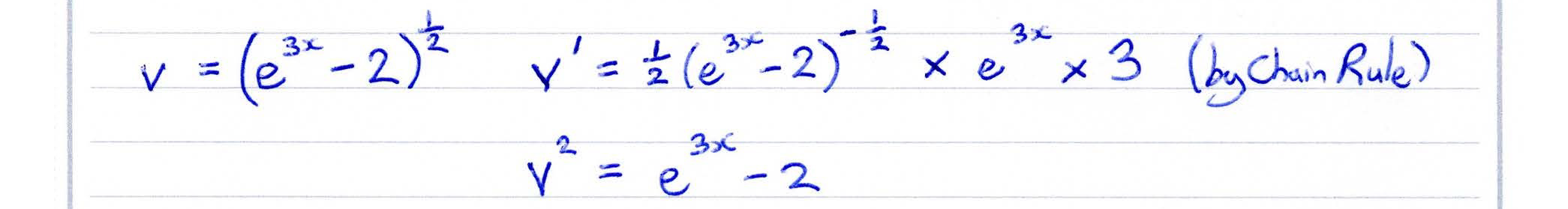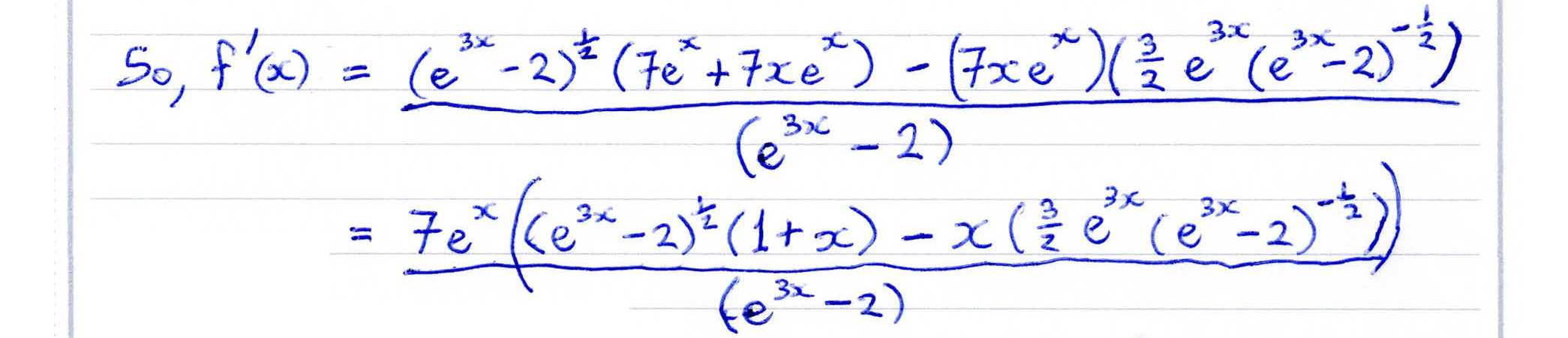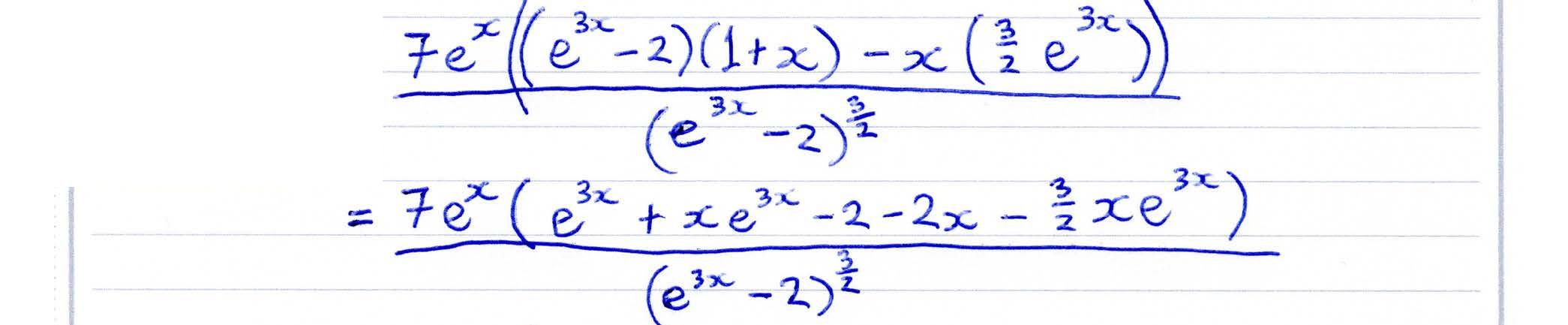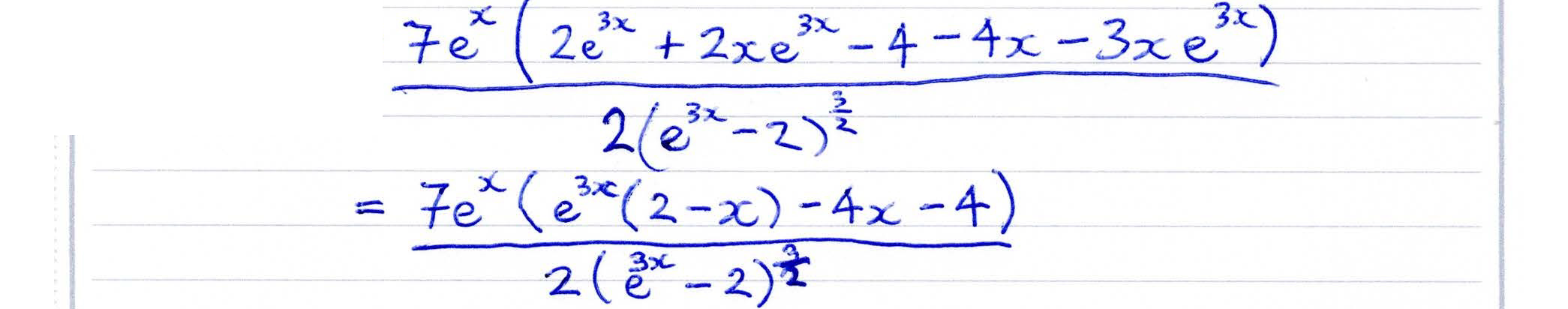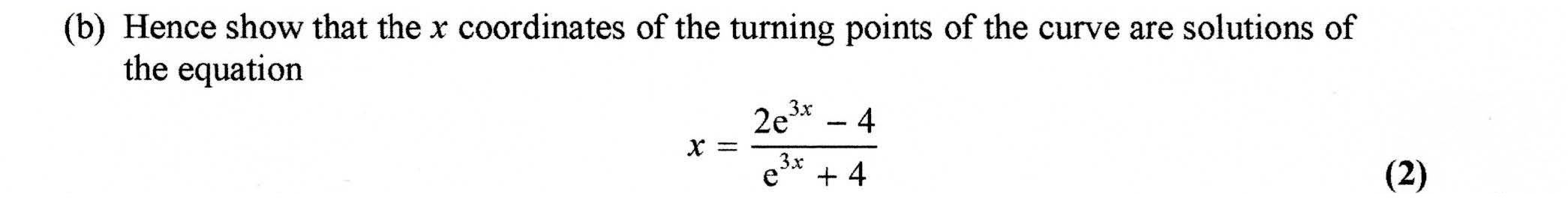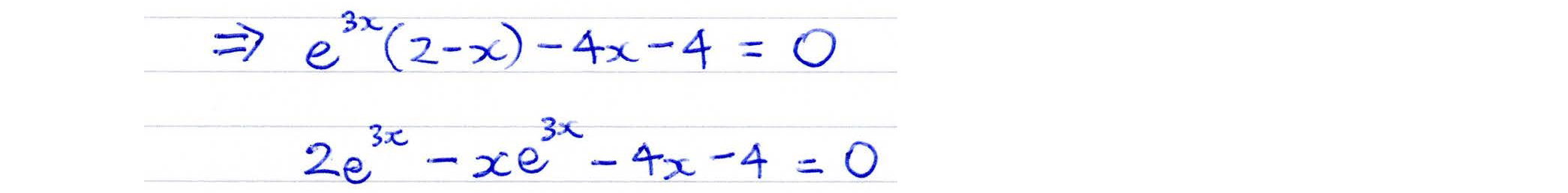Selected: Edexcel A Level Maths - Pure Maths
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads

- Theory Theory Revision
- OCR (A) Qs OCR (A) Qs
- Edexcel Qs Edexcel Qs
- AQA Qs AQA Qs
- OCR MEI Qs OCR MEI Qs
- fx-991EX Use of fx-991EX
- JsxGraph JsxGraph
-
Jun 23 AS
P1 Q 4 Jun 23 AS
Jun 23 AS
P1 Q 4
-
Jun 22 A2
P3 Q 5 a Jun 22 A2
Jun 22 A2
P3 Q 5 a
-
Nov 21 A2
P2 Q 1 Nov 21 A2
Nov 21 A2
P2 Q 1
-
Nov 20 A2
P2 Q 1 a Nov 20 A2
Nov 20 A2
P2 Q 1 a
-
Nov 20 A2
P1 Q 8 Nov 20 A2
Nov 20 A2
P1 Q 8
-
Jun 19 A2
P2 Q 1 a Jun 19 A2
Jun 19 A2
P2 Q 1 a
-
Jun 19 A2
P1 Q 12 Jun 19 A2
Jun 19 A2
P1 Q 12
-
Jun 19 A2
P3 Q 4 a Jun 19 A2
Jun 19 A2
P3 Q 4 a
-
Jun 19 AS
P1 Q 7 Jun 19 AS
Jun 19 AS
P1 Q 7
-
Jun 17 A2
P1 Q 10 Jun 17 A2
Jun 17 A2
P1 Q 10
OCR (A) H230/01 Jun 2023 AS Exam Q. 4
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/03 Jun 2022 A2 Exam Q. 5 a
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Nov 2021 A2 Exam Q. 1
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Nov 2020 A2 Exam Q. 1 a
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/01 Nov 2020 A2 Exam Q. 8
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/02 Jun 2019 A2 Exam Q. 1 a
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/01 Jun 2019 A2 Exam Q. 12
 12 marks in 14:24 min.
12 marks in 14:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/03 Jun 2019 A2 Exam Q. 4 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H230/01 Jun 2019 AS Exam Q. 7
 11 marks in 13:12 min.
11 marks in 13:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR (A) H240/01 Jun 2017 A2 Sample Exam Q. 10
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 24 A2
P1 Q 5 Jun 24 A2
Jun 24 A2
P1 Q 5
-
Jun 24 A2
P2 Q 6 Jun 24 A2
Jun 24 A2
P2 Q 6
-
Jan 24 A2
P2 Q 9 Jan 24 A2
Jan 24 A2
P2 Q 9
-
Jun 23 A2
P1 Q 15 ab Jun 23 A2
Jun 23 A2
P1 Q 15 ab
-
Jan 23 A2
P2 Q 14 Jan 23 A2
Jan 23 A2
P2 Q 14
-
Jan 23 A2
P2 Q 2 a Jan 23 A2
Jan 23 A2
P2 Q 2 a
-
Jun 22 A2
P2 Q 12 Jun 22 A2
Jun 22 A2
P2 Q 12
-
Jun 22 A2
P1 Q 8 ab Jun 22 A2
Jun 22 A2
P1 Q 8 ab
-
Dec 21 A2
P2 Q 12 a Dec 21 A2
Dec 21 A2
P2 Q 12 a
-
Dec 21 A2
P1 Q 7 a Dec 21 A2
Dec 21 A2
P1 Q 7 a
-
Dec 21 A2
P2 Q 9 Dec 21 A2
Dec 21 A2
P2 Q 9
-
Nov 21 A2
P1 Q 14 Nov 21 A2
Nov 21 A2
P1 Q 14
-
Nov 21 A2
P1 Q 4 a Nov 21 A2
Nov 21 A2
P1 Q 4 a
-
Oct 20 A2
P2 Q 13 Oct 20 A2
Oct 20 A2
P2 Q 13
-
Oct 20 A2
P2 Q 7 a Oct 20 A2
Oct 20 A2
P2 Q 7 a
-
Oct 20 A2
P1 Q 9 a Oct 20 A2
Oct 20 A2
P1 Q 9 a
-
Jun 19 A2
P2 Q 11 a Jun 19 A2
Jun 19 A2
P2 Q 11 a
-
Jun 19 A2
P2 Q 11 a Jun 19 A2
Jun 19 A2
P2 Q 11 a
-
Jun 19 A2
P1 Q 12 a Jun 19 A2
Jun 19 A2
P1 Q 12 a
-
Jun 19 A2
P1 Q 12 a Jun 19 A2
Jun 19 A2
P1 Q 12 a
-
Jun 19 A2
P1 Q 14 Jun 19 A2
Jun 19 A2
P1 Q 14
-
Jun 19 A2
P1 Q 14 Jun 19 A2
Jun 19 A2
P1 Q 14
-
Jun 19 A2
P1 Q 3 Jun 19 A2
Jun 19 A2
P1 Q 3
-
Jun 19 A2
P1 Q 3 Jun 19 A2
Jun 19 A2
P1 Q 3
-
Jan 19 A2
P1 Q 11 Jan 19 A2
Jan 19 A2
P1 Q 11
-
Jan 19 A2
P2 Q 11 a Jan 19 A2
Jan 19 A2
P2 Q 11 a
-
Jun 18 A2
P1 Q 5 Jun 18 A2
Jun 18 A2
P1 Q 5
-
May 18 A2
P2 Q 6 ab May 18 A2
May 18 A2
P2 Q 6 ab
-
May 17 A2
P1 Q 15 a May 17 A2
May 17 A2
P1 Q 15 a
-
May 17 A2
P2 Q 3 May 17 A2
May 17 A2
P2 Q 3
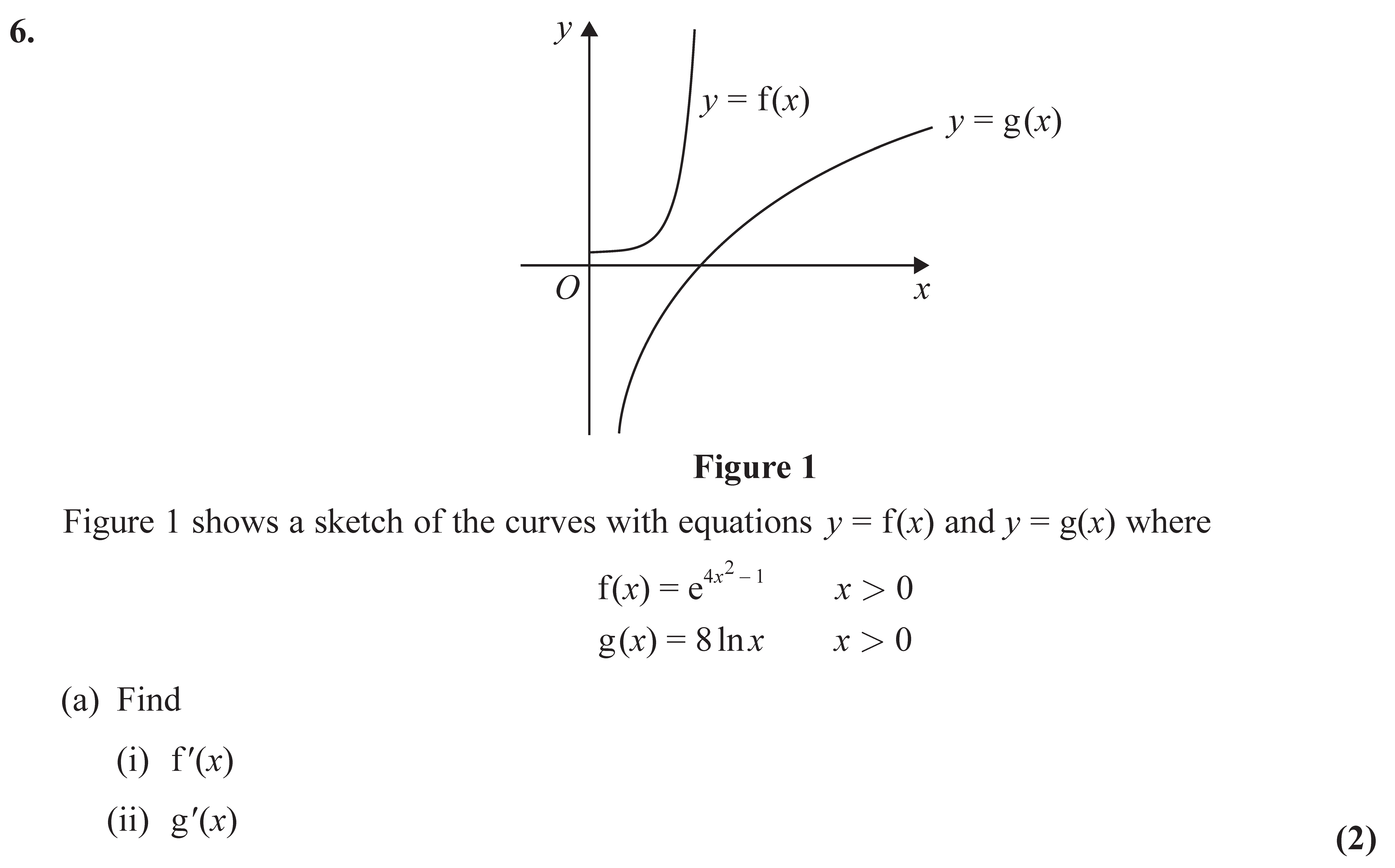
Edexcel 9MA0/01 Jun 2024 A2 Exam Q. 5
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2024 A2 Exam Q. 6
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2024 A2 Mock Q. 9
 10 marks in 12:00 min.
10 marks in 12:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2023 A2 Exam Q. 15 ab
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2023 A2 Mock Q. 14
 10 marks in 12:00 min.
10 marks in 12:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2023 A2 Mock Q. 2 a
 2 marks in 2:24 min.
2 marks in 2:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2022 A2 Exam Q. 12
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2022 A2 Exam Q. 8 ab
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 12 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Dec 2021 A2 Mock Q. 7 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Dec 2021 A2 Mock Q. 9
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 14
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 4 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 13
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 7 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Oct 2020 A2 Exam Q. 9 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2019 A2 Exam Q. 11 a
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2019 A2 Shadow Exam Q. 11 a
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Exam Q. 12 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Shadow Exam Q. 12 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Shadow Exam Q. 14
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Exam Q. 14
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Shadow Exam Q. 3
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2019 A2 Exam Q. 3
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (1)
Request * Pop-Up Working * (1)
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 11
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2019 A2 Mock Q. 11 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2018 A2 Exam Q. 5
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 May 2018 A2 Mock Q. 6 ab
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 15 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 May 2017 A2 Sample Exam Q. 3
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 24 A2
P3 Q 4 Jun 24 A2
Jun 24 A2
P3 Q 4
-
Jun 24 A2
P2 Q 5 Jun 24 A2
Jun 24 A2
P2 Q 5
-
Jun 24 A2
P1 Q 6 Jun 24 A2
Jun 24 A2
P1 Q 6
-
Jun 23 A2
P3 Q 5 Jun 23 A2
Jun 23 A2
P3 Q 5
-
Jun 22 A2
P1 Q 15 a Jun 22 A2
Jun 22 A2
P1 Q 15 a
-
Jun 22 AS
P2 Q 3 Jun 22 AS
Jun 22 AS
P2 Q 3
-
Jun 22 A2
P1 Q 5 Jun 22 A2
Jun 22 A2
P1 Q 5
-
Nov 21 A2
P1 Q 10 a Nov 21 A2
Nov 21 A2
P1 Q 10 a
-
Nov 21 AS
P1 Q 2 Nov 21 AS
Nov 21 AS
P1 Q 2
-
Nov 21 AS
P1 Q 6 Nov 21 AS
Nov 21 AS
P1 Q 6
-
Nov 20 AS
P2 Q 3 Nov 20 AS
Nov 20 AS
P2 Q 3
-
Nov 20 AS
P1 Q 8 Nov 20 AS
Nov 20 AS
P1 Q 8
-
Jun 19 AS
P2 Q 1 Jun 19 AS
Jun 19 AS
P2 Q 1
-
Jun 19 A2
P1 Q 13 Jun 19 A2
Jun 19 A2
P1 Q 13
-
Jun 19 A2
P1 Q 16 ab Jun 19 A2
Jun 19 A2
P1 Q 16 ab
-
Jun 19 A2
P1 Q 2 Jun 19 A2
Jun 19 A2
P1 Q 2
-
Jun 18 A2
P1 Q 1 Jun 18 A2
Jun 18 A2
P1 Q 1
-
Jun 18 A2
P3 Q 2 Jun 18 A2
Jun 18 A2
P3 Q 2
-
Jun 17 A2
P1 Q 2 Jun 17 A2
Jun 17 A2
P1 Q 2
-
Jun 17 A2
P1 Q 9 Jun 17 A2
Jun 17 A2
P1 Q 9
-
Jun 17 AS
P2 Q 9 Jun 17 AS
Jun 17 AS
P2 Q 9
AQA 7357/3 Jun 2024 A2 Exam Q. 4
 2 marks in 2:24 min.
2 marks in 2:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/2 Jun 2024 A2 Exam Q. 5
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2024 A2 Exam Q. 6
 2 marks in 2:24 min.
2 marks in 2:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/3 Jun 2023 A2 Exam Q. 5
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2022 A2 Exam Q. 15 a
 16 marks in 19:12 min.
16 marks in 19:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2022 AS Exam Q. 3
 5 marks in 5:38 min.
5 marks in 5:38 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2022 A2 Exam Q. 5
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Nov 2021 A2 Exam Q. 10 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/1 Nov 2021 AS Exam Q. 2
 1 mark in 1:08 min.
1 mark in 1:08 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/1 Nov 2021 AS Exam Q. 6
 7 marks in 7:52 min.
7 marks in 7:52 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Nov 2020 AS Exam Q. 3
 3 marks in 3:22 min.
3 marks in 3:22 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/1 Nov 2020 AS Exam Q. 8
 8 marks in 9:00 min.
8 marks in 9:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2019 AS Exam Q. 1
 1 mark in 1:08 min.
1 mark in 1:08 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2019 A2 Exam Q. 13
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2019 A2 Exam Q. 16 ab
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2019 A2 Exam Q. 2
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2018 A2 Exam Q. 1
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/3 Jun 2018 A2 Exam Q. 2
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2017 A2 Sample Exam Q. 2
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2017 A2 Sample Exam Q. 9
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7356/2 Jun 2017 AS Sample Exam Q. 9
 5 marks in 5:38 min.
5 marks in 5:38 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Nov 21 A2
P2 Q 14 Nov 21 A2
Nov 21 A2
P2 Q 14
-
Nov 20 A2
P1 Q 4 Nov 20 A2
Nov 20 A2
P1 Q 4
-
Jun 19 A2
P3 Q 10 Jun 19 A2
Jun 19 A2
P3 Q 10
-
Jun 19 A2
P2 Q 2 Jun 19 A2
Jun 19 A2
P2 Q 2
-
Jun 18 A2
P1 Q 13 i Jun 18 A2
Jun 18 A2
P1 Q 13 i
-
Jun 17 A2
P1 Q 4 Jun 17 A2
Jun 17 A2
P1 Q 4
OCR MEI H640/02 Nov 2021 A2 Exam Q. 14
 13 marks in 15:36 min.
13 marks in 15:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Nov 2020 A2 Exam Q. 4
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/03 Jun 2019 A2 Exam Q. 10
 4 marks in 6:24 min.
4 marks in 6:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/02 Jun 2019 A2 Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Jun 2018 A2 Exam Q. 13 i
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Jun 2017 A2 Exam Q. 4
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
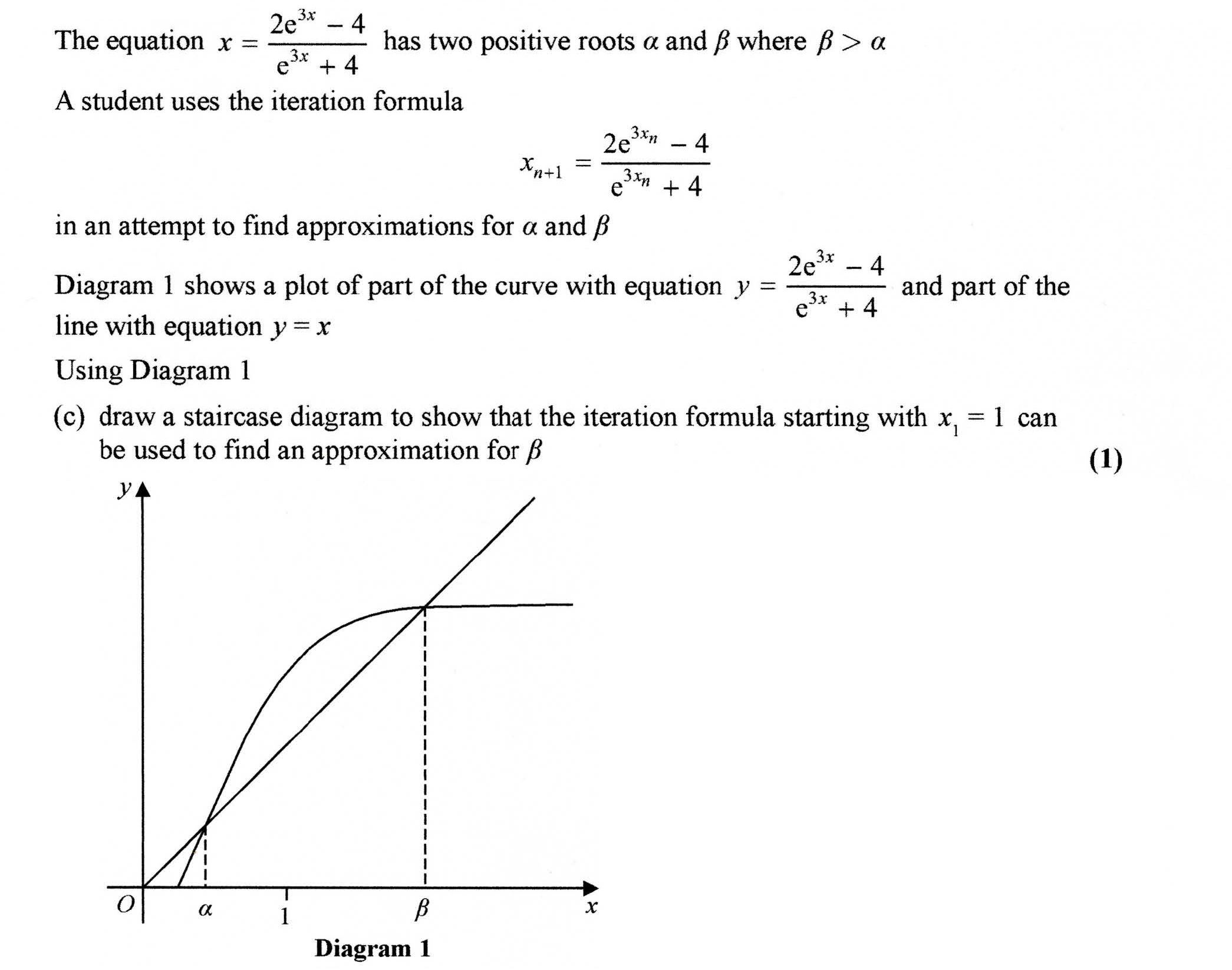
Checking solutions to quadratic equations in differentiation

- Composite Functions (A2) Composite Functions (A2)
- Product Rule (A2) Product Rule (A2)
- Quotient Rule (A2) Quotient Rule (A2)
1st and 2nd Derivatives of Composite Functions
This display allows you to investigate the first and second derivatives of some composite functions.
Visualise the Product Rule
The function $ {x ^ 2} \, (x−1) $ is a product of $ {x ^ 2} $ and $ (x−1) $.
The derivative of $ {x ^ 2} $ is $ 2x $ and the derivative of $ (x−1) $ is $ 1 $.
So, is the derivative of $ {x ^ 2} \, (x−1) $ equal to $ 2x(1) = 2x $, or $ 2x + 1 $, or something else?
This display allows you to visualise the curve $ {x ^ 2} \, (x − 1) $, as well as many other products of functions. You can use it to visualise the "Product Rule" which defines how gradient functions are derived for products of functions.
This display allows you to visualise the curve $ {x ^ 2} \, (x − 1) $, as well as many other products of functions. You can use it to visualise the "Product Rule" which defines how gradient functions are derived for products of functions.
Visualise the Quotient Rule
The connection between a function $ h(x) $ and it derivative $ h'(x) $ is much harder to see when the function
$ h(x) $ is a quotient of two other functions.
This display allows you to visualise the curve $ { x \over x + 1 } $, as well as many other quotients of functions. You can use it to visualise the "Quotient Rule" which defines how gradient functions are derived for quotients of functions.
This display allows you to visualise the curve $ { x \over x + 1 } $, as well as many other quotients of functions. You can use it to visualise the "Quotient Rule" which defines how gradient functions are derived for quotients of functions.