Selected: -
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads
AS & A2 (Whole Course) - All Questions - Casio fx-991EX
Register / Login for More / Subscribe for All Without Ads

- Theory Theory Revision
- AQA Qs AQA Qs
- Edexcel Qs Edexcel Qs
- OCR Qs OCR Qs
- OCR MEI Qs OCR MEI Qs
- GeoGebra GeoGebra
- JsxGraph JsxGraph
-
Jun 24 A2
P1 Q 16 Jun 24 A2
Jun 24 A2
P1 Q 16
-
Jun 23 A2
P3 Q 2 Jun 23 A2
Jun 23 A2
P3 Q 2
-
Jun 23 A2
P1 Q 5 Jun 23 A2
Jun 23 A2
P1 Q 5
-
Jun 22 A2
P1 Q 14 a Jun 22 A2
Jun 22 A2
P1 Q 14 a
-
Nov 20 A2
P1 Q 11 Nov 20 A2
Nov 20 A2
P1 Q 11
-
Jun 19 A2
P1 Q 14 a Jun 19 A2
Jun 19 A2
P1 Q 14 a
-
Jun 17 A2
P3 Q 7 Jun 17 A2
Jun 17 A2
P3 Q 7
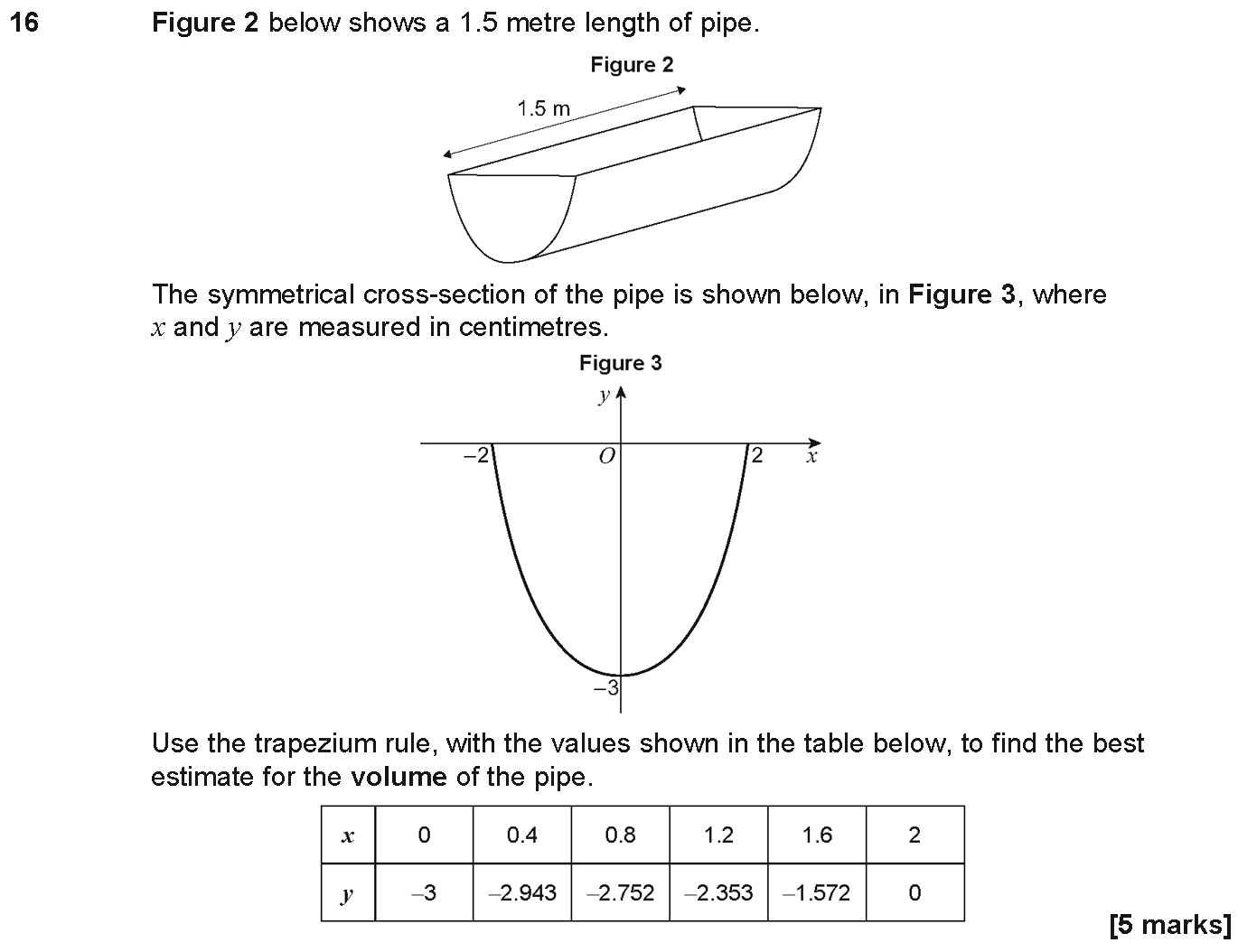
AQA 7357/1 Jun 2024 A2 Exam Q. 16
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
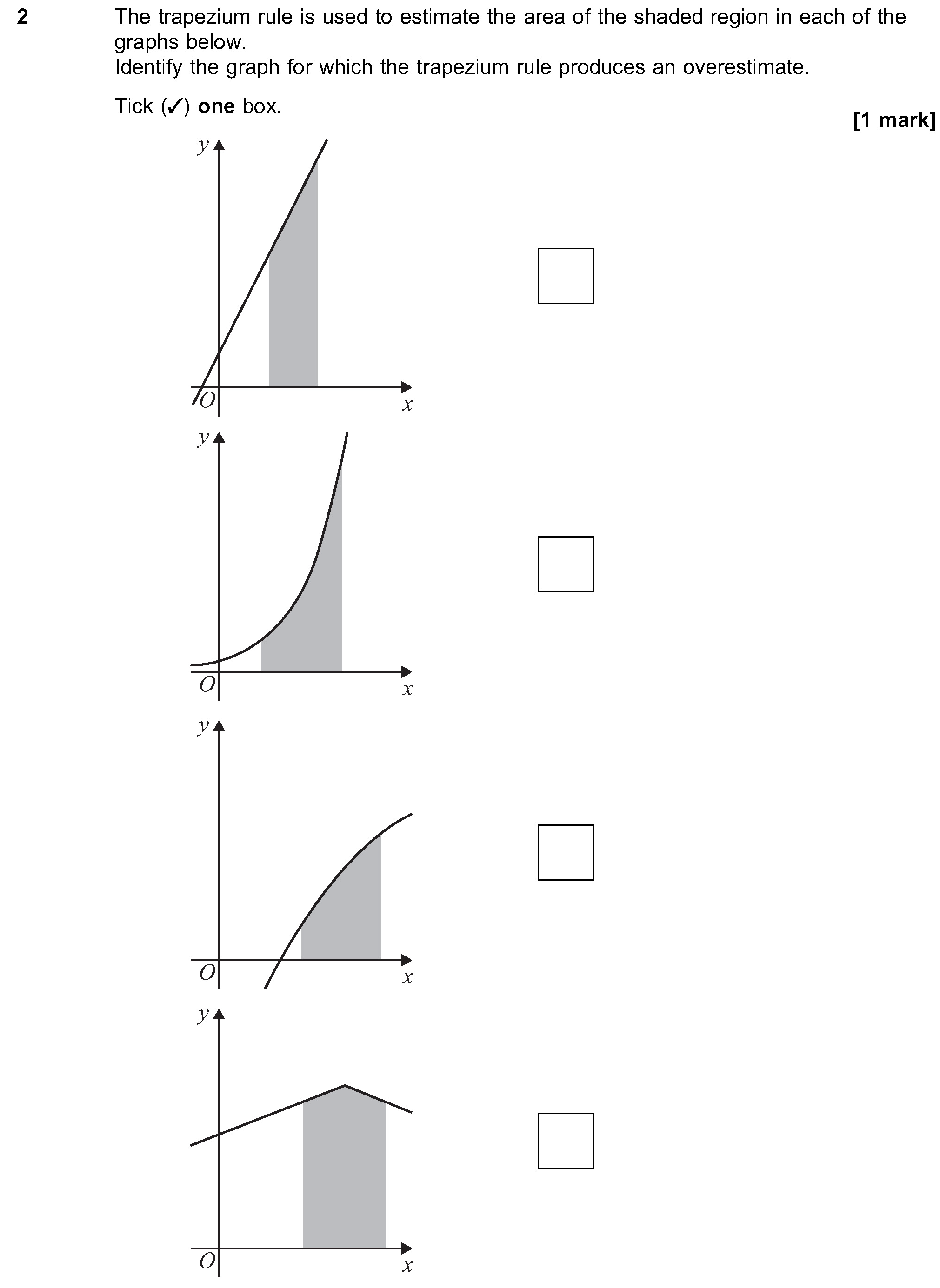
AQA 7357/3 Jun 2023 A2 Exam Q. 2
 1 mark in 1:12 min.
1 mark in 1:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
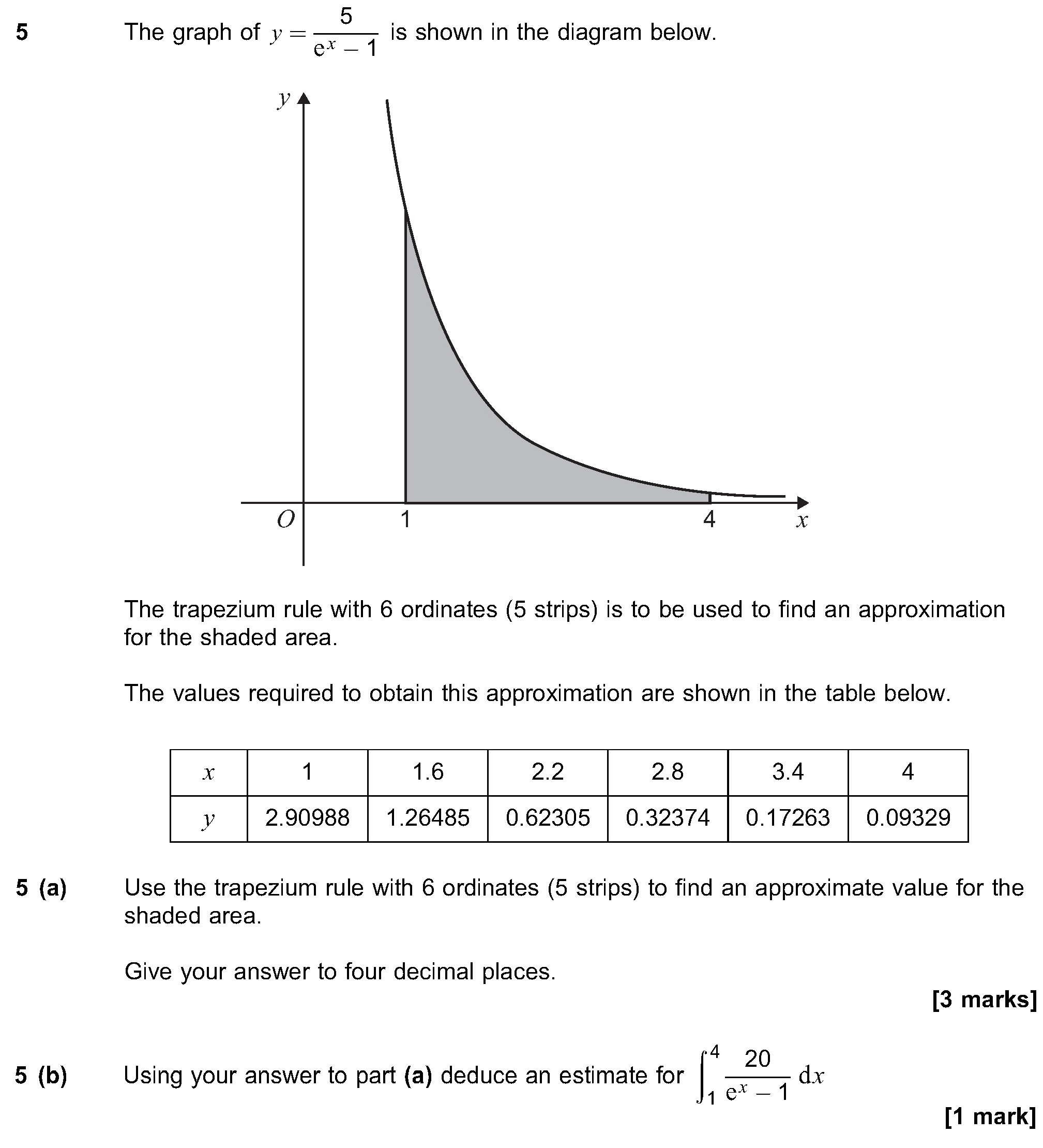
AQA 7357/1 Jun 2023 A2 Exam Q. 5
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2022 A2 Exam Q. 14 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Nov 2020 A2 Exam Q. 11
 9 marks in 10:48 min.
9 marks in 10:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/1 Jun 2019 A2 Exam Q. 14 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
AQA 7357/3 Jun 2017 A2 Sample Exam Q. 7
 12 marks in 14:24 min.
12 marks in 14:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jan 24 A2
P1 Q 7 Jan 24 A2
Jan 24 A2
P1 Q 7
-
Jun 23 A2
P1 Q 5 Jun 23 A2
Jun 23 A2
P1 Q 5
-
Jan 23 A2
P2 Q 3 Jan 23 A2
Jan 23 A2
P2 Q 3
-
Jun 22 A2
P2 Q 5 Jun 22 A2
Jun 22 A2
P2 Q 5
-
Dec 21 A2
P1 Q 3 Dec 21 A2
Dec 21 A2
P1 Q 3
-
Nov 21 A2
P1 Q 11 a Nov 21 A2
Nov 21 A2
P1 Q 11 a
-
Oct 20 A2
P2 Q 1 Oct 20 A2
Oct 20 A2
P2 Q 1
-
Mar 20 A2
P1 Q 9 Mar 20 A2
Mar 20 A2
P1 Q 9
-
Jun 19 A2
P2 Q 2 Jun 19 A2
Jun 19 A2
P2 Q 2
-
Jun 19 A2
P2 Q 2 Jun 19 A2
Jun 19 A2
P2 Q 2
-
Jan 19 A2
P1 Q 1 Jan 19 A2
Jan 19 A2
P1 Q 1
-
May 18 A2
P1 Q 1 May 18 A2
May 18 A2
P1 Q 1
-
May 17 A2
P1 Q 14 ab May 17 A2
May 17 A2
P1 Q 14 ab
Edexcel 9MA0/01 Jan 2024 A2 Mock Q. 7
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jun 2023 A2 Exam Q. 5
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jan 2023 A2 Mock Q. 3
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2022 A2 Exam Q. 5
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Dec 2021 A2 Mock Q. 3
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Nov 2021 A2 Exam Q. 11 a
 3 marks in 3:36 min.
3 marks in 3:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Oct 2020 A2 Exam Q. 1
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Mar 2020 A2 Mock Q. 9
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2019 A2 Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/02 Jun 2019 A2 Shadow Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 Jan 2019 A2 Mock Q. 1
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (1)
Request * Pop-Up Working * (1)
Edexcel 9MA0/01 May 2018 A2 Mock Q. 1
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Edexcel 9MA0/01 May 2017 A2 Sample Exam Q. 14 ab
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 24 A2
P1 Q 1 Jun 24 A2
Jun 24 A2
P1 Q 1
-
Jun 22 A2
P1 Q 1 Jun 22 A2
Jun 22 A2
P1 Q 1
-
Nov 21 A2
P2 Q 6 Nov 21 A2
Nov 21 A2
P2 Q 6
-
Nov 20 A2
P1 Q 10 a Nov 20 A2
Nov 20 A2
P1 Q 10 a
-
Jun 19 A2
P3 Q 4 c Jun 19 A2
Jun 19 A2
P3 Q 4 c
-
Jun 18 A2
P1 Q 2 Jun 18 A2
Jun 18 A2
P1 Q 2
-
Jun 17 A2
P3 Q 2 Jun 17 A2
Jun 17 A2
P3 Q 2
OCR H240/01 Jun 2024 A2 Exam Q. 1
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/01 Jun 2022 A2 Exam Q. 1
 6 marks in 7:12 min.
6 marks in 7:12 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/02 Nov 2021 A2 Exam Q. 6
 5 marks in 6:00 min.
5 marks in 6:00 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/01 Nov 2020 A2 Exam Q. 10 a
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/03 Jun 2019 A2 Exam Q. 4 c
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/01 Jun 2018 A2 Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR H240/03 Jun 2017 A2 Sample Exam Q. 2
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
-
Jun 22 A2
P2 Q 14 Jun 22 A2
Jun 22 A2
P2 Q 14
-
Nov 20 A2
P1 Q 8 Nov 20 A2
Nov 20 A2
P1 Q 8
-
Jun 19 A2
P2 Q 4 Jun 19 A2
Jun 19 A2
P2 Q 4
-
Jun 18 A2
P1 Q 13 iv v Jun 18 A2
Jun 18 A2
P1 Q 13 iv v
-
Jun 17 A2
P1 Q 6 Jun 17 A2
Jun 17 A2
P1 Q 6
OCR MEI H640/02 Jun 2022 A2 Exam Q. 14
 8 marks in 9:36 min.
8 marks in 9:36 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Nov 2020 A2 Exam Q. 8
 7 marks in 8:24 min.
7 marks in 8:24 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/02 Jun 2019 A2 Exam Q. 4
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Jun 2018 A2 Exam Q. 13 iv v
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
OCR MEI H640/01 Jun 2017 A2 Exam Q. 6
 4 marks in 4:48 min.
4 marks in 4:48 min.
Vote:
 (0)
(0)
 (0)
(0)
 (0)
(0)
Request * Pop-Up Working * (0)
Request * Pop-Up Working * (0)
Under-estimation and over-estimation with the trapezium rule
Trapezium Rule Approximation for Difficult Integrals 1
The method of finding the area under a curve by splitting it up into strips is often referred to as a "Riemann
sum". The value of a definite integral can be estimated using various numerical
methods. This is particularly useful when the integral is difficult or
impossible to integrate. The method consists of dividing the area into strips.
The trapezium rule (or trapezoidal rule in the USA) is one such method. The
area of each strip is estimated by taking it to be approximately a
trapezium.
The trapezium method uses this formula:
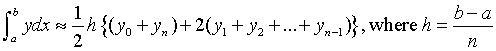
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
The trapezium method uses this formula:
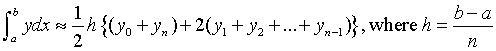
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
Trapezium Rule Approximation for Difficult Integrals 2
Functions such as $\color{blue}{y = {e^{ - {x^2}}}}$ and $\color{blue}{y = \sin \left( {x^2} \right)}$
cannot be integrated by basic methods.
However, their definite integrals can be estimated using numerical methods such as the trapezium rule (or trapezoidal rule in the USA) which is presented here.
The method consists of dividing the area into strips. The area of each strip is estimated by taking it to be approximately a trapezium.
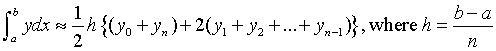
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.
However, their definite integrals can be estimated using numerical methods such as the trapezium rule (or trapezoidal rule in the USA) which is presented here.
The method consists of dividing the area into strips. The area of each strip is estimated by taking it to be approximately a trapezium.
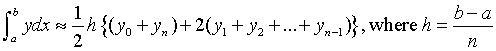
With the display, you should see how the accuracy of the estimate increases as the number of intervals increases.
With the display, you should also see how the trapezium rule overestimates where the curve is concave upwards, and underestimates where the curve is convex upwards.